早教吧作业答案频道 -->数学-->
已知:如图,OA=OB,OC=OD,∠AOB=∠COD.(1)求证:AC=BD;(2)求证:OE平分∠AED.
题目详情
已知:如图,OA=OB,OC=OD,∠AOB=∠COD.
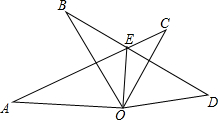
(1)求证:AC=BD;
(2)求证:OE平分∠AED.

(1)求证:AC=BD;
(2)求证:OE平分∠AED.
▼优质解答
答案和解析
证明:(1)∵∠AOB=∠COD,
∴∠AOC=∠BDO.
在△AOC和△BOD中
,
∴△AOC≌△BOD.
∴AC=BD.
(2)连接BA、CD.
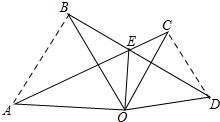
∵△AOC≌△BOD,
∴∠ACO=∠BDO,∠OAC=∠OBD.
∵∠ACO和∠BDO在OE的同侧,且∠ACO=∠BDO,
∴点E、O、D、C共圆.
∴∠OED=∠OCD.
同理:∠AEO=∠ABO.
∵OC=OD,
∴∠CCD=∠ODC.
∴∠COD=
(180°-∠COD).
同理:∠ABO=
(180°-∠AOB).
∵∠AOB=∠COD,
∴∠COD=∠ABO.
∴∠AEO=∠DEO.
∴EO平分∠AED.
∴∠AOC=∠BDO.
在△AOC和△BOD中
|
∴△AOC≌△BOD.
∴AC=BD.
(2)连接BA、CD.

∵△AOC≌△BOD,
∴∠ACO=∠BDO,∠OAC=∠OBD.
∵∠ACO和∠BDO在OE的同侧,且∠ACO=∠BDO,
∴点E、O、D、C共圆.
∴∠OED=∠OCD.
同理:∠AEO=∠ABO.
∵OC=OD,
∴∠CCD=∠ODC.
∴∠COD=
| 1 |
| 2 |
同理:∠ABO=
| 1 |
| 2 |
∵∠AOB=∠COD,
∴∠COD=∠ABO.
∴∠AEO=∠DEO.
∴EO平分∠AED.
看了 已知:如图,OA=OB,OC...的网友还看了以下:
∵EM是⊙O的切线,怎么推出EB•EC=EM2①?,看题后回答.(2005•温州)如图,已知四边形 2020-05-21 …
证明o(x^m)+o(x^n)=o(x^m)(x→0)(n>m>0)过程请详细一些,谢谢啦请问其中 2020-06-12 …
已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.(1)如图1,若点O在边BC 2020-06-12 …
如果O+O=U+U+U,O+Z=U+U+U+U,那么Z+Z+U=()个O.如果设U=6,那么O=( 2020-06-18 …
已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.(1)如图1,若点O在边BC 2020-07-24 …
圆O与圆O'相交与A,B两点,过点B作CD垂直于AB,分别交圆O与圆O'于点C.D.(1)求证:A 2020-07-31 …
以下说法正确的是()A.在用综合法证明的过程中,每一个分步结论都是结论成立的必要条件B.在用综合法 2020-08-01 …
大气臭氧层的反应是:O+O3=2O2△H,该反应的能量变化如图所示,下列叙述中,正确的是()A.O+ 2020-10-31 …
如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(2012•临沂)如图 2020-11-13 …
《假如给我三天阳光》中有意义的句子,并附感悟,字数(包括原句)250——350不等如题,O(∩∩)O 2020-12-19 …