早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,BC=6,点P从点B出发沿线段BA移动,同时,点Q从点C出发沿线段AC的延长线移动,当点P运动到A时,点P、Q随即停止运动,若点P、Q移动的速度相同,PQ与直线BC相交于点D.
题目详情
如图,在△ABC中,AB=AC,BC=6,点P从点B出发沿线段BA移动,同时,点Q从点C出发沿线段AC的延长线移动,当点P运动到A时,点P、Q随即停止运动,若点P、Q移动的速度相同,PQ与直线BC相交于点D.
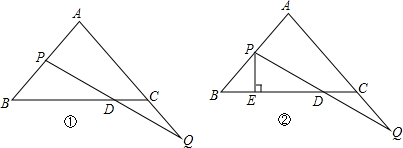
(1)如图①,当点P自点B出发在线段BA上运动是,过点P作AC的平行交BC于点F,连接PC、FQ,判断四边形PFQC的形状,并证明你的结论.
(2)如图②,过点P作PE⊥BC,垂足为E,请说明在点P、Q在移动的过程中,DE长度保持不变.
(1)如图①,当点P自点B出发在线段BA上运动是,过点P作AC的平行交BC于点F,连接PC、FQ,判断四边形PFQC的形状,并证明你的结论.
(2)如图②,过点P作PE⊥BC,垂足为E,请说明在点P、Q在移动的过程中,DE长度保持不变.

▼优质解答
答案和解析
(1)如图①中,四边形PFQC是平行四边形.
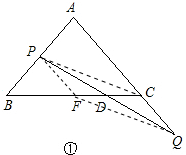
理由:∵AB=AC,
∴∠B=∠ACB,
∵PF∥AQ,
∴∠PFB=∠ACB=∠B,∠DPF=∠DQC,
∴PB=PF=CQ,
在△DPF和△DQC中,
,
∴△DPF≌△DQC,
∴DP=DQ,DF=DC,
∴四边形PFQC是平行四边形.
(2)如图②中,过点P作PF∥AC交BC于F,
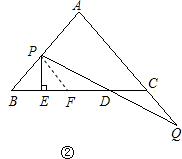
∵△PBF为等腰三角形,
∴PB=PF,
∵PE⊥BF
∴BE=EF,
由(1)可知FD=DC,
∴ED=EF+FD=
BF+
FC=
(BF+FC)=
BC=3,
∴ED为定值,

理由:∵AB=AC,
∴∠B=∠ACB,
∵PF∥AQ,
∴∠PFB=∠ACB=∠B,∠DPF=∠DQC,
∴PB=PF=CQ,
在△DPF和△DQC中,
|
∴△DPF≌△DQC,
∴DP=DQ,DF=DC,
∴四边形PFQC是平行四边形.
(2)如图②中,过点P作PF∥AC交BC于F,

∵△PBF为等腰三角形,
∴PB=PF,
∵PE⊥BF
∴BE=EF,
由(1)可知FD=DC,
∴ED=EF+FD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴ED为定值,
看了 如图,在△ABC中,AB=A...的网友还看了以下:
在数轴上表示数a,b的点AB到表示-2的点C的距离相等,且点A点B间距离为6个长度单位,则a+b- 2020-04-27 …
如图,已知直线y=-x-(k+1)与双曲线y=k/x相交于B,C两点,与x轴相交于A点,BM垂直y 2020-05-14 …
RT△ABO中,顶点A是双曲线y=k/x与直线y=-x+(k+1)在第四象限的交点,AB垂直x轴与 2020-05-15 …
正五边形广场ABCDE周长2000m,甲乙两人分别从A,C两点同时出发,沿A—B—C—D—E方向绕 2020-05-16 …
在矩形ABCD中,已知AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F; 2020-05-16 …
已知a的倒数为-1/2,b的相反数是0,表示有理数c的点,到原点的距离是c的倒数,求c/(a-b) 2020-05-16 …
如图,已知数轴上有三点A.B.C,AB=二分之一AC,点C对应的数是200.(1)若BC=300求 2020-05-23 …
在正点电荷Q的电厂中,A,B,C是同一电场线上的三个点,A场强100N/C,C场强36N/C,B是 2020-06-12 …
已知如图,在平面直角坐标系中,点O是坐标原点,矩形OABC的顶点B在第一象限,点A,C的坐标分别为 2020-06-14 …
在平面直角坐标系xOy中,抛物线y=ax²+bx+c与x轴交于A、B两点(点A在点B的左侧),与y 2020-06-14 …