已知函数f（x）=|x|+2，x<1x+2x，x≥1.，设a∈R，若关于x的不等式f（x）≥|x2+a|在R上恒成立，则a的取值范围是（）A.[-2，2]B.[-23，2]C.[-2，23]D.[-23，23]

Question

已知函数f（x）=

|x|+2，x<1

x+(2)/(x)，x≥1.

，设a∈R，若关于x的不等式f（x）≥|(x)/(2)+a|在R上恒成立，则a的取值范围是（　　）

A. [-2，2]

B. [-2

√(3)，2]

C. [-2，2

√(3)]

D. [-2

√(3)，2√(3)]

Answer 1

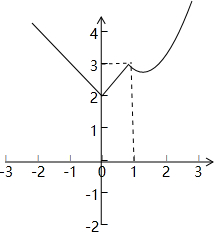根据题意，函数f（x）=

|x|+2，x<1

x+(2)/(x)，x≥1.

的图象如图：
令g（x）=|(x)/(2)+a|，其图象与x轴相交与点（-2a，0），
在区间（-∞，-2a）上为减函数，在（-2a，+∞）为增函数，
若不等式f（x）≥|(x)/(2)+a|在R上恒成立，则函数f（x）的图象在
g（x）上的上方或相交，
则必有f（0）≥g（0），
即2≥|a|，
解可得-2≤a≤2，
故选：A．