早教吧作业答案频道 -->数学-->
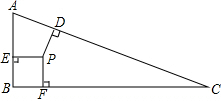
如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,PE⊥AB、PF⊥BC、PD⊥AC,垂足分别为E、F、D,求PD的长.
题目详情
如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,PE⊥AB、PF⊥BC、PD⊥AC,垂足分别为E、F、D,求PD的长.

▼优质解答
答案和解析
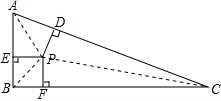 连接AP,BP,CP.
连接AP,BP,CP.
设PE=PF=PD=x.
∵△ABC中,∠B=90°,两直角边AB=7,BC=24,
∴AC=25.
∵S△ABC=
×AB×CB=84,
S△ABC=
AB×x+
AC×x+
BC×x=
(AB+BC+AC)•x=
×56x=28x,
则28x=84,
x=3.
故PD的长为3.
 连接AP,BP,CP.
连接AP,BP,CP.设PE=PF=PD=x.
∵△ABC中,∠B=90°,两直角边AB=7,BC=24,
∴AC=25.
∵S△ABC=
| 1 |
| 2 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则28x=84,
x=3.
故PD的长为3.
看了 如图,△ABC中,∠B=90...的网友还看了以下:
P(A/B)+P(A非/B非)=1证明AB独立我这样证:原始=P(A/B)+1-P(A/B非)=1 2020-04-06 …
已知P(A)=0.3,P(B)=0.5,P(AB)=0.15,验证P(B┃A)=P(B),P(B┃ 2020-06-12 …
已知P(A)=0.3,P(B)=0.5,P(AB)=0.15,验证:P(B|A)=P(B),P(B 2020-06-22 …
设P(A)>0,则下面结论正确的:A、P(B|A)P(A)≥P(A)‐P(B)B、P(B|A)P( 2020-07-18 …
已知P(AB)=P(A)+P(B)证明P(A的相反事件B的相反事件)=P(A的相反事件)+P(B的 2020-07-20 …
设A、B、C为事件,P(ABC)>0,如果P(AB|C)=P(A|C)P(B|C),则()A.P( 2020-07-20 …
P(B/A)表示什么意思?是代表在A事件发生的条件下,B事件发生的概率?可是又怎么理解这句话呢?怎 2020-07-30 …
设A,B是两个随机事件,且0<P(A)<1,P(B)>0,P(B|A)=P(B|.A),则必有()A 2020-11-01 …
概率论中,若事件A,B相互独立,则P(A-B)=0,P(B-A)=P(B)-P(A).这是怎么证的? 2020-12-01 …
求证若B⊂A,则P(A-B)=P(A)-P(B)且P(A)≥P(B)……谢谢……给出一种解法,但是需 2020-12-01 …