早教吧作业答案频道 -->数学-->
如图1,在等腰Rt△ACB中,∠ACB=90°,AC=BC;在等腰Rt△DCE中,∠DCE=90°,CD=CE;点D、E分别在边BC、AC上,连接AD、BE,点N是线段BE的中点,连接CN与AD交于点G.(1)若CN=6.5,CE=5,求BD的值.(2)
题目详情
如图1,在等腰Rt△ACB中,∠ACB=90°,AC=BC;在等腰Rt△DCE中,∠DCE=90°,CD=CE;点D、E分别在边BC、AC上,连接AD、BE,点N是线段BE的中点,连接CN与AD交于点G.
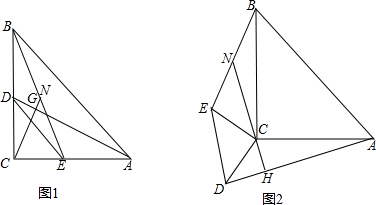
(1)若CN=6.5,CE=5,求BD的值.
(2)求证:CN⊥AD.
(3)把等腰Rt△DCE绕点C转至如图2位置,点N是线段BE的中点,延长NC交AD于点H,请问(2)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由.

(1)若CN=6.5,CE=5,求BD的值.
(2)求证:CN⊥AD.
(3)把等腰Rt△DCE绕点C转至如图2位置,点N是线段BE的中点,延长NC交AD于点H,请问(2)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
▼优质解答
答案和解析
(1)∵∠ACB=90°,点N是线段BE的中点,
∴BE=2CN=13,
∵CE=5,
∴BC=
=12,
∵CD=CE=5,
∴BD=BC-CD=7;
(2)在△ACD与△BCE中,
,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠ACB=90°,点N是线段BE的中点,
∴CN=BN,
∴∠CBE=∠NCD,
∴∠NCD=∠CAD,
∵∠NCD+∠NCA=90°,
∴∠CAG+∠GCA=90°,
∴∠CGA=90°,
∴CN⊥AD;
(3)(2)中的结论还成立,如图2,延长CN到F使FN=CN,连接BF,
在△CEN与△BFN中,
,
∴△CEN≌△BNF,
∴CE=BF,∠F=∠ECN,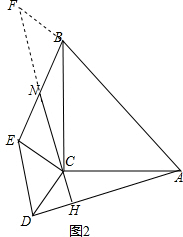
∵∠CBF=180°-∠F-∠BCF,∠DCA=360°-∠DCE-∠ACB-∠BCE=180°-∠ECF-∠BCF,
∴∠CBF=∠DCA,
∵CE=CD,
∴BF=CD,
在△ACD与△BCF中,
,
∴△ACD≌△BCF,
∴∠DAC=∠BCF,
∵∠BCF+∠ACH=90°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,
∴CN⊥AD.
∴BE=2CN=13,
∵CE=5,
∴BC=
| BE2-CE2 |
∵CD=CE=5,
∴BD=BC-CD=7;
(2)在△ACD与△BCE中,
|
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠ACB=90°,点N是线段BE的中点,
∴CN=BN,
∴∠CBE=∠NCD,
∴∠NCD=∠CAD,
∵∠NCD+∠NCA=90°,
∴∠CAG+∠GCA=90°,
∴∠CGA=90°,
∴CN⊥AD;
(3)(2)中的结论还成立,如图2,延长CN到F使FN=CN,连接BF,
在△CEN与△BFN中,
|
∴△CEN≌△BNF,
∴CE=BF,∠F=∠ECN,

∵∠CBF=180°-∠F-∠BCF,∠DCA=360°-∠DCE-∠ACB-∠BCE=180°-∠ECF-∠BCF,
∴∠CBF=∠DCA,
∵CE=CD,
∴BF=CD,
在△ACD与△BCF中,
|
∴△ACD≌△BCF,
∴∠DAC=∠BCF,
∵∠BCF+∠ACH=90°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,
∴CN⊥AD.
看了 如图1,在等腰Rt△ACB中...的网友还看了以下:
已知a,b,c均为整数,且a-b的绝对值的三次方+c-a的绝对值的平方=1,求a-c的绝对值+c- 2020-04-05 …
依据下列各题的条件,判断△abc与△a'b'c'是否相似,并说明理由(1)∠c=∠c'=90°,∠ 2020-05-16 …
有机物A是一种重要的有机合成原料.以有机物A为原料合成G(医药中间体和材料中间体)的路线如图所示: 2020-06-08 …
如果下面的DNA双螺旋从左向右进行转录,指出那条链是编码链.并写出转录产物的顺序?5’-A-T-C 2020-06-26 …
数据库应用题已知有关系模式R(U,F),其中U=ABCDEG,F={AD→E,AC→E,CB→G, 2020-07-02 …
1.已知a+b+c=0,a^2+b^2+c^=1,求:①ab+bc+ac的值②a^4+b^4+c^ 2020-07-09 …
python组合问题有一个二维数列list=[['a','b'],['c','d','e'],'f 2020-07-17 …
某生物基因单链的一段是┅G-C-A-G-A-C-A-A-A┅若以此链为模板,经转录翻译形成的多肽链上 2020-12-18 …
a^n+a^(n-1)+a^(n-2)+……+a^1+a^0这个是什么来着?a^n+a^(n-1)+ 2021-01-04 …
1.若2x²-kx²+3被2x+1除后余2,求k的值2.已知a,b,c,d是四个不同的有理数,且(a 2021-01-20 …