早教吧作业答案频道 -->数学-->
在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE为矩形;(2)若AE=3,BF=4,AF平分∠DAB,求BE的长.
题目详情
在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
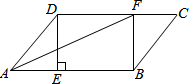
(1)求证:四边形BFDE为矩形;
(2)若AE=3,BF=4,AF平分∠DAB,求BE的长.

(1)求证:四边形BFDE为矩形;
(2)若AE=3,BF=4,AF平分∠DAB,求BE的长.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴DF∥BE,
又∵DF=BE,
∴四边形BFDE是平行四边形,
又∵DE⊥AB,
∴∠DEB=90°,
∴平行四形BFDE是矩形;
(2) ∵四边形BFDE是矩形,
∴DF∥AB,DE=BF=4,DF=BE,
∴∠DAF=∠FAB,
又∵AF平分∠DAB,
∴∠DAF=∠FAB,
∴∠DFA=∠DAF,
∴DA=DF,
又∵DE⊥AB,
∴∠DEA=90°,
在Rt△ADE中
AD=
=
=5,
∴BE=5.
∴DF∥BE,
又∵DF=BE,
∴四边形BFDE是平行四边形,
又∵DE⊥AB,
∴∠DEB=90°,
∴平行四形BFDE是矩形;
(2) ∵四边形BFDE是矩形,
∴DF∥AB,DE=BF=4,DF=BE,
∴∠DAF=∠FAB,
又∵AF平分∠DAB,
∴∠DAF=∠FAB,
∴∠DFA=∠DAF,
∴DA=DF,
又∵DE⊥AB,
∴∠DEA=90°,
在Rt△ADE中
AD=
| AE2+DE2 |
| 32+42 |
∴BE=5.
看了 在平行四边形ABCD中,过点...的网友还看了以下:
已知(a+b)平方=3,(a-b)平方=5,求a平方+ab+b平方的值 2020-04-05 …
分式的加减法2a/5a平方b+3b/10a平方b平方3/(x-1)平方-3x/(x-1)平方 2020-05-13 …
(1)在平行四边形ABCD中,∠A-∠B=60°,则∠A=,∠B=.(2)在平行四边形ABCD中, 2020-05-20 …
有下列哪项情况者暂不宜上避孕环 ( )A.月经后3~7天B.平产3个月后C.剖宫产后6个月D.人工流 2020-06-07 …
如图,在平面直角坐标系中,有平行四边形ABCD,且A(-1,0),B(0,3),C(3,0),BD 2020-06-13 …
已知ab的平方=—3,则—ab(a的平方*b的五次方—a*b的3次方—b)一个正方形边长增加3厘米 2020-06-29 …
1.在△ABC中,a=x,b=x√3,A=45度,则满足此条件的三角形个数为多少?A.0B.1C. 2020-07-19 …
平行四边形ABCO四个定点坐标分别是A(√3,√3)B(3√3,√3)C(2√3,0)O(0,0) 2020-07-30 …
a平方+b平方+3≥ab+(根号3)(a+b)用综合法证明:a平方+b平方+3≥ab+(根号3)( 2020-08-01 …
其中“原”命题与“逆”命题都是真命题的有:1若a>0,b>0则a+b>02平行四边形的对角线互相平 2020-08-01 …