早教吧作业答案频道 -->数学-->
如图:△ABC是O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作O的切线交AB的延长线于点D.(1)求证:CD=CB;(2)如果O的半径为2,求AC的长.
题目详情
如图:△ABC是 O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作 O的切线交AB的延长线于点D.
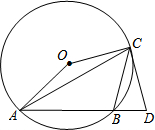
(1)求证:CD=CB;
(2)如果 O的半径为
,求AC的长.

(1)求证:CD=CB;
(2)如果 O的半径为
| 2 |
▼优质解答
答案和解析
(1)证明:连接OB,则∠AOB=2∠ACB=2×45°=90°,
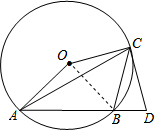 ∵OA=OB,
∵OA=OB,
∴∠OAB=OBA=45°,
∵∠AOC=150°,OA=OC,
∴∠OCA=∠OAC=15°,
∴∠OCB=∠OCA+∠ACB=60°,
∴△OBC是等边三角形,
∴∠BOC=∠OBC=60°,
∴∠CBD=180°-∠OBA-∠OBC=75°,
∵CD是 O的切线,
∴OC⊥CD,
∴∠D=360°-∠OBD-∠BOC-∠OCD=360°-(60°+75°)-60°-90°=75°,
∴∠CBD=∠D,
∴CB=CD;
(2)在Rt△AOB中,AB=
OA=
×
=2,
∵CD是 O的切线,
∴∠DCB=∠CAD,
∵∠D是公共角,
∴△DBC∽△DCA,
∴
=
,
∴CD2=AD•BD=BD•(BD+AB),
∵CD=BC=OC=
,
∴2=BD•(2+BD),
解得:BD=
-1,
∴AC=AD=AB+BD=
+1.
 ∵OA=OB,
∵OA=OB,∴∠OAB=OBA=45°,
∵∠AOC=150°,OA=OC,
∴∠OCA=∠OAC=15°,
∴∠OCB=∠OCA+∠ACB=60°,
∴△OBC是等边三角形,
∴∠BOC=∠OBC=60°,
∴∠CBD=180°-∠OBA-∠OBC=75°,
∵CD是 O的切线,
∴OC⊥CD,
∴∠D=360°-∠OBD-∠BOC-∠OCD=360°-(60°+75°)-60°-90°=75°,
∴∠CBD=∠D,
∴CB=CD;
(2)在Rt△AOB中,AB=
| 2 |
| 2 |
| 2 |
∵CD是 O的切线,
∴∠DCB=∠CAD,
∵∠D是公共角,
∴△DBC∽△DCA,
∴
| CD |
| AD |
| BD |
| CD |
∴CD2=AD•BD=BD•(BD+AB),
∵CD=BC=OC=
| 2 |
∴2=BD•(2+BD),
解得:BD=
| 3 |
∴AC=AD=AB+BD=
| 3 |
看了 如图:△ABC是O的内接三角...的网友还看了以下:
多边形和半圆形?如一个半圆形接在正多边形上,半圆形的弧线刚好外切于正多边形,但是直线又从正多边行中 2020-05-14 …
高中生物:关于半透膜的基本知识理解》》》此句话:“另外,在扩散过程中,两种物质运动可以通过半透膜, 2020-05-15 …
物理变压器题目啊5.B如图所示,在绕制变压器时,某人将两个线圈绕在图示变压器铁芯的左右两个臂上,当 2020-05-16 …
诗中具体写春半如秋的句子是什么(柳宗元的柳州榕叶落尽偶题) 2020-05-21 …
通观柳宗元的(柳州榕叶落尽偶题)是什么原因使作者产生春半如秋的感觉对乱字作简要赏析 2020-05-21 …
柳州榕叶落尽偶题)是什么原因使作者产生春半如秋的感觉 2020-05-21 …
柳州榕叶落尽偶题赏析-译文1.通观全诗,是什么原因使诗人产生“春半如秋”的感觉?2.有人说三、四句 2020-05-21 …
的鉴赏(1)通过全诗,是什么原因使诗人产生“春半如秋”的感觉?(2)有人说三,四两句将“在物之境” 2020-05-21 …
黄土高原地区在自然、人文上是哪些因素的过渡地带(如在降水上,是半干旱与半湿润的过渡地带)越全面越好 2020-06-05 …
一电场强度为E的均匀电场,E的方向与沿x轴正向,如图所示,则通过图中一半径为R的半一电场强度为E的 2020-06-08 …