早教吧作业答案频道 -->数学-->
如图,直线AB与CD相交于O,OF是∠BOD的平分线,OE⊥OF.(1)若∠BOE=64°,求∠DOF和∠AOC的度数;(2)试问∠COE与∠BOE之间有怎样的大小关系?为什么?
题目详情
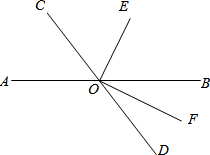 如图,直线AB与CD相交于O,OF是∠BOD的平分线,OE⊥OF.
如图,直线AB与CD相交于O,OF是∠BOD的平分线,OE⊥OF.(1)若∠BOE=64°,求∠DOF和∠AOC的度数;
(2)试问∠COE与∠BOE之间有怎样的大小关系?为什么?
▼优质解答
答案和解析
考点:
对顶角、邻补角 角平分线的定义 垂线
专题:
分析:
(1)根据余角的性质,可得∠BOF的度数,根据角平分线的性质,可得∠DOF的度数、∠BOD的度数,根据对顶角相等,可得答案;(2)根据角的和差,可得∠COE的度数,根据角的大小比较,可得答案.
(1)由OE⊥OF,∠BOE=64°,得∠BCF=∠EOF-∠BOE=90°-64°=26°.由OF是∠BOD的平分线,得∠DOF=∠BOF=26°,∠BOD=2∠BOF=52°,由对顶角相等,得∠AOC=∠BOD=52°;(2)∠COE=∠BOE,理由如下:由角的和差,得∠COB+∠BOD=180°,即12∠COB+12∠BOD=12×180°=90°①,∠EOF=∠BOE+∠BOF=90°,∠BOF=12∠BOD,∠BOE+12∠BOD=90°②①-②,得12∠COB-∠BOE=0.即12∠COB=∠BOE.
点评:
本题考查了对顶角、邻补角,利用了角的和差,角平分线的性质,对顶角相等的性质.
考点:
对顶角、邻补角 角平分线的定义 垂线
专题:
分析:
(1)根据余角的性质,可得∠BOF的度数,根据角平分线的性质,可得∠DOF的度数、∠BOD的度数,根据对顶角相等,可得答案;(2)根据角的和差,可得∠COE的度数,根据角的大小比较,可得答案.
(1)由OE⊥OF,∠BOE=64°,得∠BCF=∠EOF-∠BOE=90°-64°=26°.由OF是∠BOD的平分线,得∠DOF=∠BOF=26°,∠BOD=2∠BOF=52°,由对顶角相等,得∠AOC=∠BOD=52°;(2)∠COE=∠BOE,理由如下:由角的和差,得∠COB+∠BOD=180°,即12∠COB+12∠BOD=12×180°=90°①,∠EOF=∠BOE+∠BOF=90°,∠BOF=12∠BOD,∠BOE+12∠BOD=90°②①-②,得12∠COB-∠BOE=0.即12∠COB=∠BOE.
点评:
本题考查了对顶角、邻补角,利用了角的和差,角平分线的性质,对顶角相等的性质.
看了 如图,直线AB与CD相交于O...的网友还看了以下:
请高手帮解决下面几何题,在正方体ABCD-A/B/C/D中,P是线段B/C上一个动点,下列命题错误 2020-05-19 …
铜导线与铝导线的导电性能相比,()。A.铜导线好B.铝导线好C.两种导线一样D.两种导线差不多 2020-05-29 …
f(mx-a)与函数f(b-mx)的图象关于直线(a+b)/2m对称,f(a+mx)和f(b-mx 2020-07-22 …
关于渐开线和摆线的叙述正确的是()A.只有圆才有渐开线B.渐开线和摆线的定义是一样的,只是绘图 2020-07-31 …
探讨过空间一点P做直线与一对异面直线都成等角.这样的直线有几条若2条异面直线a,b所成角为β.则过 2020-08-02 …
怎样用函数思想证明除数不为0用一次函数和二次函数已知函数y=ax2+bx+c对称轴是直线x=-b/2 2020-11-03 …
如图,直线a∥b,点A为直线a上的动点,点B为直线a,b之间的定点,点C为直线b上的定点.(1)当∠ 2020-11-03 …
法拉第曾做过这样一个实验:在一个软铁圆环上绕两个互相绝缘的线圈A和B,如图所示,用一根铜导线将B线圈 2020-11-05 …
学了异面直线的概念和作法后,老师出了下面一道题:“已知平面α,β,a,b是异面直线,a∈α,b∈β, 2020-11-06 …
(2009•揭阳模拟)两个匝数不同的线圈绕在同一个圆筒上,如图所示,它们的匝数nA>nB.当一个条形 2020-11-12 …