如图，平面直角坐标系中，将含30°的三角尺的直角顶点C落在第二象限。其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm（1）若OB=6cm．①

Question

如图，平面直角坐标系中，将含 30° 的三角尺的直角顶点 C 落在第二象限。其斜边两端点 A 、 B 分别落在 x 轴、 y 轴上，且 AB=12 cm

（1）        若 OB=6 cm ．

①      求点 C 的坐标；

②      若点 A 向右滑动的距离与点 B 向上滑动的距离相等，求滑动的距离；

（2）        点 C 与点 O 的距离的最大值 =         cm .

 

Answer 1

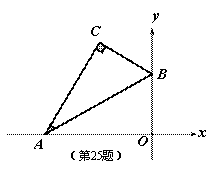
(1) ① 过点 C 作 y 轴的垂线，垂足为 D ，

        在 R t △ AOB 中， AB=12 ， OB=6 ，则 BC=6 ，

        ∴∠ BAO=30° ，∠ ABO=60° ，

        又∠ CBA=60° ，∴∠ CBD=60° ，∠ BCD=30° ，

        ∴ BD=3 ， CD=3 ．

        ② 设点 A 向右滑动的距离为 x ，根据题意得点 B 向动的距离也为 x

AO=12× cos ∠ BAO=12× cos 30°=6 ．

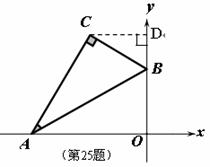∴ A'O=6 － x ， B'O=6 ＋ x ， A'B'=AB=12

在 △ A'O B' 中 ， 由勾股定理得 ，

(6 － x )² ＋ (6 ＋ x )²=12²

解得 ， x =6( － 1 )

∴滑动的距离为 6( － 1 ) ．

(2) 设点 C 的坐标为 ( x y ) ，过 C 作 CE ⊥ x 轴， CD ⊥ y 轴， 垂足分别为 E ， D

则 OE= － x ， OD= y ，

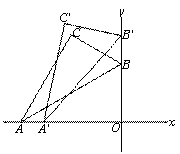∵∠ ACE ＋ ∠ BCE=90° ，∠ DCB ＋ ∠ BCE=90°

∴∠ ACE= ∠ DCB ，

又∵∠ AEC= ∠ BDC=90° ，

∴△ ACE ∽ △ BCD

∴ ，即 ，

∴ y = － x ，

OC²= x ² ＋ y ²= x ² ＋ ( － x )²=4 x ²

∴当︱ x ︱取最大值时即 C 到 y 轴距离最大时 OC² 有最

大 值，即 OC 取最大值，如图，即当 C'B' 转到与 y 轴垂时

．此时 OC=12 ．