如图，某城市小区有一个矩形休闲广场，AB=20米，广场的一角是半径为16米的扇形BCE绿化区域，为了使小区居民能够更好的在广场休闲放松，现决定在广场上安置两排休闲椅，其中一排是穿越

Question

如图，某城市小区有一个矩形休闲广场，AB=20米，广场的一角是半径为16米的扇形BCE绿化区域，为了使小区居民能够更好的在广场休闲放松，现决定在广场上安置两排休闲椅，其中一排是穿越广场的双人靠背直排椅MN（宽度不计），点M在线段AD上，并且与曲线CE相切；另一排为单人弧形椅沿曲线CN（宽度不计）摆放．已知双人靠背直排椅的造价每米为2a元，单人弧形椅的造价每米为a元，记锐角∠NBE=θ，总造价为W元．

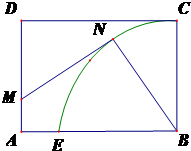
（1）试将W表示为θ的函数W（θ），并写出cosθ的取值范围；
（2）如何选取点M的位置，能使总造价W最小．

Answer 1

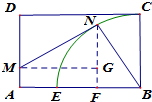（1）过N作AB的垂线，垂足为F；过M作NF的垂线，垂足为G．
在Rt△BNF中，BF=16cosθ，则MG=20-16cosθ
在Rt△MNG中，MN=(20-16cosθ)/(sinθ)，
由题意易得CN=16((π)/(2)-θ)，
因此，W(θ)=2a•(20-16cosθ)/(sinθ)+16a((π)/(2)-θ)，cosθ∈(0，(4)/(5))；
（2）W，(θ)=-16a+8a(4-5cosθ)/(sin2θ) =8a((2cosθ-1)(cosθ-2))/(sin2θ)
令W′（θ）=0，cosθ=(1)/(2)，因为(θ1，(π)/(2))，所以θ=(π)/(3)．
设锐角θ₁满足cosθ1=(4)/(5)，θ1∈(0，(π)/(3))
当θ∈(θ1，(π)/(3))时，W，（θ）<0，W（θ）单调递减；
当θ∈((π)/(3)，(π)/(2))时，W，（θ）>0，W（θ）单调递增．
所以当θ=(π)/(3)，总造价W最小，最小值为(16√(3)+(8π)/(3))a，
此时MN=8√(3)，NG=4√(3)，NF=8√(3)，
因此当AM=4

作业帮用户 2016-12-01

扫描下载二维码

©2019 作业帮 联系方式：[e-mail]  作业帮协议