早教吧作业答案频道 -->数学-->
设函数.(1)若x=1是f(x)的极大值点,求a的取值范围.(2)当a=0,b=-1时,函数F(x)=f(x)-λx2有唯一零点,求正数λ的值.
题目详情
设函数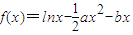 .
.
(1)若x=1是f(x)的极大值点,求a的取值范围.
(2)当a=0,b=-1时,函数F(x)=f(x)-λx 2 有唯一零点,求正数λ的值.
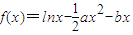 .
.(1)若x=1是f(x)的极大值点,求a的取值范围.
(2)当a=0,b=-1时,函数F(x)=f(x)-λx 2 有唯一零点,求正数λ的值.
▼优质解答
答案和解析
分析:
(Ⅰ)f(x)的定义域为(0,+∞),,由f'(1)=0,得b=1-a.所以,由此能求出a的取值范围.(Ⅱ)因为函数F(x)=f(x)-λx2有唯一零点,即λx2-lnx-x=0有唯一实数解,设g(x)=λx2-lnx-x,则.令g'(x)=0,2λx2-x-1=0.由此进行分类讨论,能求出λ.
(Ⅰ)f(x)的定义域为(0,+∞),,由f'(1)=0,得b=1-a.∴.…(2分)①若a≥0,由f'(x)=0,得x=1.当0<x<1时,f'(x)>0,此时f(x)单调递增;当x>1时,f'(x)<0,此时f(x)单调递减.所以x=1是f(x)的极大值点.…(4分)②若a<0,由f'(x)=0,得x=1,或x=.因为x=1是f(x)的极大值点,所以>1,解得-1<a<0.综合①②:a的取值范围是a>-1.…(6分)(Ⅱ)因为函数F(x)=f(x)-λx2有唯一零点,即λx2-lnx-x=0有唯一实数解,设g(x)=λx2-lnx-x,则.令g'(x)=0,2λx2-x-1=0.因为λ>0,所以△=1+8λ>0,方程有两异号根设为x1<0,x2>0.因为x>0,所以x1应舍去.当x∈(0,x2)时,g'(x)<0,g(x)在(0,x2)上单调递减;当x∈(x2,+∞)时,g'(x)>0,g(x)在(x2,+∞)单调递增.当x=x2时,g'(x2)=0,g(x)取最小值g(x2).…(9分)因为g(x)=0有唯一解,所以g(x2)=0,则即因为λ>0,所以2lnx2+x2-1=0(*)设函数h(x)=2lnx+x-1,因为当x>0时,h(x)是增函数,所以h(x)=0至多有一解.因为h(1)=0,所以方程(*)的解为x2=1,代入方程组解得λ=1.…(12分)
点评:
本题考查函数的单调性、极值、零点等知识点的应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.
分析:
(Ⅰ)f(x)的定义域为(0,+∞),,由f'(1)=0,得b=1-a.所以,由此能求出a的取值范围.(Ⅱ)因为函数F(x)=f(x)-λx2有唯一零点,即λx2-lnx-x=0有唯一实数解,设g(x)=λx2-lnx-x,则.令g'(x)=0,2λx2-x-1=0.由此进行分类讨论,能求出λ.
(Ⅰ)f(x)的定义域为(0,+∞),,由f'(1)=0,得b=1-a.∴.…(2分)①若a≥0,由f'(x)=0,得x=1.当0<x<1时,f'(x)>0,此时f(x)单调递增;当x>1时,f'(x)<0,此时f(x)单调递减.所以x=1是f(x)的极大值点.…(4分)②若a<0,由f'(x)=0,得x=1,或x=.因为x=1是f(x)的极大值点,所以>1,解得-1<a<0.综合①②:a的取值范围是a>-1.…(6分)(Ⅱ)因为函数F(x)=f(x)-λx2有唯一零点,即λx2-lnx-x=0有唯一实数解,设g(x)=λx2-lnx-x,则.令g'(x)=0,2λx2-x-1=0.因为λ>0,所以△=1+8λ>0,方程有两异号根设为x1<0,x2>0.因为x>0,所以x1应舍去.当x∈(0,x2)时,g'(x)<0,g(x)在(0,x2)上单调递减;当x∈(x2,+∞)时,g'(x)>0,g(x)在(x2,+∞)单调递增.当x=x2时,g'(x2)=0,g(x)取最小值g(x2).…(9分)因为g(x)=0有唯一解,所以g(x2)=0,则即因为λ>0,所以2lnx2+x2-1=0(*)设函数h(x)=2lnx+x-1,因为当x>0时,h(x)是增函数,所以h(x)=0至多有一解.因为h(1)=0,所以方程(*)的解为x2=1,代入方程组解得λ=1.…(12分)
点评:
本题考查函数的单调性、极值、零点等知识点的应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.
看了 设函数.(1)若x=1是f(...的网友还看了以下:
已知a大于2,求证:log(a-1)a大于loga(a+1)log(a-1)a中a-1是底数,lo 2020-04-05 …
如果a大于2,则|a+3|=?|2-a|=? 2020-04-06 …
a大于2,b大于2,a加b小于a乘b 证明题!用求商法证明. 2020-04-11 …
作业中有疑问的几题,在线等,谢谢1.化简/a-b/-/a+b/=2.当a大于2时,不等式(2-a) 2020-04-27 …
当-1大于A大于2时,化简「3A-2「A+1「当-1小于A小于2时,化简「3A-2「A+1「 2020-04-27 …
按向量a把点(2,-1)平移到(-2,1),则a把点(-2,1)平移到 2020-05-16 …
小明的妈妈用一个最多能盛2.5kg水的塑料桶装满豆油,则桶内豆油的质量[]A.大于2.5kgB.小 2020-05-17 …
小明的妈妈用一个最多能盛2.5kg水的塑料桶装满豆油,则桶内豆油的质量()A.大于2.5kgB.小 2020-05-17 …
再问几个高二不等式题错用均值不等式的是B(x方+2)/根下(x方+1)大于等于2。Clgx+log 2020-05-19 …
如图为一突触的结构,在a、d两点连接一个灵敏电流计.已知ab=bd,若分别刺激b、c两点,灵敏电流 2020-07-07 …