早教吧作业答案频道 -->数学-->
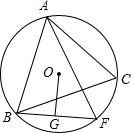
已知△ABC内接于O,F是弧BC上一点,OG⊥BF于点G,且OG=12AC.证明:AF⊥BC.
题目详情
已知△ABC内接于 O,F是弧
上一点,OG⊥BF于点G,且OG=
AC.证明:AF⊥BC.
 |
| BC |
| 1 |
| 2 |

▼优质解答
答案和解析
证明:如图,作直径FM,连结BM、AM,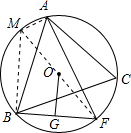
则∠MAF=90°,
∵OG⊥BF,
∴BG=GF,
在△FBM中,∵OF=OM,FG=GB,
∴OG=
BM,又OG=
AC,
∴BM=AC,
∴MA∥BC,
∴AF⊥BC.

则∠MAF=90°,
∵OG⊥BF,
∴BG=GF,
在△FBM中,∵OF=OM,FG=GB,
∴OG=
| 1 |
| 2 |
| 1 |
| 2 |
∴BM=AC,
∴MA∥BC,
∴AF⊥BC.
看了 已知△ABC内接于O,F是弧...的网友还看了以下:
如图,已知点A,B是椭圆x^2/a^2+y^2/b^2=1(a>b>0)的两个顶点,若点C(t,t 2020-06-21 …
15.已知Q点是双曲线x*2/a*2-y*2/b*2=1(a,b>0)上异于两顶点的以动点,F1, 2020-07-20 …
1.若集合A={y|y=x平方+2x+3},集合B={y|y=x+4/x},则A并B=2.点(根号 2020-07-30 …
已知椭圆E:x^2/a^2+y^2/b^2=1(a>b>0)的右焦点F(3,0),过点F的直线交椭 2020-07-31 …
已知椭圆x^2/a^2+y^2/b^2=1的左右两个焦点分别为F1F2,右顶点为A,上顶点为B,P 2020-07-31 …
椭圆x^2/a^2+y^2/b^2=1(a>b>0)的右焦点为F,离心率是1/2,过F作直线l交椭 2020-08-01 …
C:x^2/a^2+y^2/b^2=1的离心率为1/2,其左焦点到点p(2,1)的距离为根号10, 2020-08-01 …
矩形ABCD,AB=a,AD=b(a>b/2),点E为AD上一动点,EF⊥EC交AB于F,设AE=x 2020-11-02 …
代数点到直线距离d=PQ=|ax0+by0+c|/√(a^2+b^2)点P(x0,y0)到直线Ax+ 2020-11-06 …
已知点F是双曲线C:x^2/a^2-y^2/b^2=1(a>0,b>0)的左焦点P为右支上一点直线P 2021-01-11 …