早教吧作业答案频道 -->数学-->
如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.(1)求证:△APE是等腰直角三角形;(2)若⊙O的直径为2,求PC2+PB2的值.
题目详情
如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
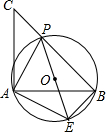
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求PC2+PB2的值.

(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求PC2+PB2的值.
▼优质解答
答案和解析
(1)证明: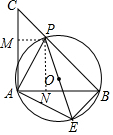 ∵AB=AC,∠BAC=90°,
∵AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°,
∴∠AEP=∠ABP=45°,
∵PE是直径,
∴∠PAB=90°,
∴∠APE=∠AEP=45°,
∴AP=AE,
∴△PAE是等腰直角三角形.
(2)作PM⊥AC于M,PN⊥AB于N,则四边形PMAN是矩形,
∴PM=AN,
∵△PCM,△PNB都是等腰直角三角形,
∴PC=
PM,PB=
PN,
∴PC2+PB2=2(PM2+PN2)=2(AN2+PN2)=2PA2=PE2=22=4.
 ∵AB=AC,∠BAC=90°,
∵AB=AC,∠BAC=90°,∴∠C=∠ABC=45°,
∴∠AEP=∠ABP=45°,
∵PE是直径,
∴∠PAB=90°,
∴∠APE=∠AEP=45°,
∴AP=AE,
∴△PAE是等腰直角三角形.
(2)作PM⊥AC于M,PN⊥AB于N,则四边形PMAN是矩形,
∴PM=AN,
∵△PCM,△PNB都是等腰直角三角形,
∴PC=
| 2 |
| 2 |
∴PC2+PB2=2(PM2+PN2)=2(AN2+PN2)=2PA2=PE2=22=4.
看了 如图,已知等腰直角三角形AB...的网友还看了以下:
P(A/B)+P(A非/B非)=1证明AB独立我这样证:原始=P(A/B)+1-P(A/B非)=1 2020-04-06 …
最大诚信原则的基本内容中,主要约束保险人的是( )。 A.告知B.保证C.弃权D.禁止反言 2020-05-21 …
不属于最大诚信原则的基本内容。A.告知B.保证C.通知D.弃权与禁止反言 2020-05-22 …
最大诚信原则的内容包括( )。A.告知B.保证C.弃权D.禁止反言 2020-05-22 …
按照惯例,投保人的告知形式包括( )。A.无限告知和询问回答告知B.保证告知和问答告知### 2020-05-22 …
最大诚信原则的基本内容中,主要约束保险人的是( )。A.告知B.保证C.弃权###SXB 2020-05-22 …
保险合同的诚信原则有( )A.告知B.保证C.弃权和禁止反言D.承诺 2020-05-22 …
已知P(AB)=P(A)+P(B)证明P(A的相反事件B的相反事件)=P(A的相反事件)+P(B的 2020-07-20 …
哪些声母可以和O组成拼音,已知b,p,m,f,w 2020-07-28 …
已知abc两两相互独立,求证P(a交b交c)=p(a)p(b)p(c)已知ab相互独立,求证a已知a 2020-12-01 …