早教吧作业答案频道 -->数学-->
如图,AB是O的直径,点D是AE上一点,且∠BDE=∠CBE,BD与AE交于点F.(1)求证:BC是O的切线;(2)若BD平分∠ABE,求证:DE2=DF•DB;(3)在(2)的条件下,延长ED、BA交于点P,若PA=AO,DE=2,
题目详情
如图,AB是 O的直径,点D是
上一点,且∠BDE=∠CBE,BD与AE交于点F.
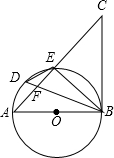
(1)求证:BC是 O的切线;
(2)若BD平分∠ABE,求证:DE2=DF•DB;
(3)在(2)的条件下,延长ED、BA交于点P,若PA=AO,DE=2,求PD的长.
 |
| AE |

(1)求证:BC是 O的切线;
(2)若BD平分∠ABE,求证:DE2=DF•DB;
(3)在(2)的条件下,延长ED、BA交于点P,若PA=AO,DE=2,求PD的长.
▼优质解答
答案和解析
(1)证明:∵AB是 O的直径,
∴∠AEB=90°,
∴∠EAB+∠ABE=90°,
∵∠EAB=∠BDE,∠BDE=∠CBE,
∴∠CBE+∠ABE=90°,即∠ABC=90°,
∴AB⊥BC,
∴BC是 O的切线;
(2)证明:∵BD平分∠ABE,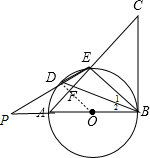
∴∠1=∠2,
而∠2=∠AED,
∴∠AED=∠1,
∵∠FDE=∠EDB,
∴△DFE∽△DEB,
∴DE:DF=DB:DE,
∴DE2=DF•DB;
(3)连结OD,如图,
∵OD=OB,
∴∠2=∠ODB,
而∠1=∠2,
∴∠ODB=∠1,
∴OD∥BE,
∴△POD∽△PBE,
∴
=
,
∵PA=AO,
∴PA=AO=BO,
∴
=
,即
=
,
∴PD=4.
∴∠AEB=90°,
∴∠EAB+∠ABE=90°,
∵∠EAB=∠BDE,∠BDE=∠CBE,
∴∠CBE+∠ABE=90°,即∠ABC=90°,
∴AB⊥BC,
∴BC是 O的切线;
(2)证明:∵BD平分∠ABE,

∴∠1=∠2,
而∠2=∠AED,
∴∠AED=∠1,
∵∠FDE=∠EDB,
∴△DFE∽△DEB,
∴DE:DF=DB:DE,
∴DE2=DF•DB;
(3)连结OD,如图,
∵OD=OB,
∴∠2=∠ODB,
而∠1=∠2,
∴∠ODB=∠1,
∴OD∥BE,
∴△POD∽△PBE,
∴
| PD |
| PE |
| PO |
| PB |
∵PA=AO,
∴PA=AO=BO,
∴
| PD |
| PE |
| 2 |
| 3 |
| PD |
| PD+2 |
| 2 |
| 3 |
∴PD=4.
看了 如图,AB是O的直径,点D是...的网友还看了以下:
设栈的初始为空,元素a,b,c,d,e,f,g依次入栈,以下出栈序列不可能出现的是A,a,b,c, 2020-05-17 …
在一个平面直角坐标系中,有一个矩形ABCD的顶点坐标分别为A(-a,b),B(-a,0),C(a, 2020-06-03 …
经科学测定,人体平均含氧65%,含碳18%,含氢10%(均以质量计),则三种元素的原子个数由多到少 2020-06-11 …
若a+b+c/d=a+b+d/c=a+c+d/b=a+c+d/a=k1)k=?2)a+b+c+d/ 2020-06-12 …
下列卤化物在浓的KOH醇溶液中脱卤化氢的反应速度最快的是?选项为:a)1-溴戊烷b)2-溴戊烷c) 2020-06-28 …
现有A,B,C,D,E,F,G七种短周期主族元素,原子序数依次增大.已知A与D,C与F分别同主族, 2020-07-07 …
设A=B=D=true,C=false,以下逻辑运算表达式值为真的有()。A.(A∧B)∨(C∧D 2020-07-18 …
四边形OABC是矩形,OA=4,OC=8,将矩形OABC沿直线Ac折叠四边形OABC是矩形,OA= 2020-07-26 …
a、b、c、d是否成比例线段是不是只能是a:b=c:ba、b、c、d成比例和a、b、d、c成比例是 2020-08-02 …
把a×b=c×d改写成比例式,不可能是()A.a:c=d:bB.a:d=c:bC.a:d=b:cD. 2020-11-28 …