早教吧作业答案频道 -->数学-->
已知在平面直角坐标系xOy中(如图),已知抛物线y=-x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.(1)求这条抛物线的表达式和点B的坐标;(2)点M在对称轴上,且位于顶点上方,设
题目详情
已知在平面直角坐标系xOy中(如图),已知抛物线y=-x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
(1)求这条抛物线的表达式和点B的坐标;
(2)点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.
(1)求这条抛物线的表达式和点B的坐标;
(2)点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.
▼优质解答
答案和解析
(1)∵抛物线的对称轴为x=1,
∴x=-
=1,即
=1,解得b=2.
∴y=-x2+2x+c.
将A(2,2)代入得:-4+4+c=2,解得:c=2.
∴抛物线的解析式为y=-x2+2x+2.
配方得:y=-(x-1)2+3.
∴抛物线的顶点坐标为(1,3).
(2)如图所示:过点A作AC⊥BM,垂足为C,则AC=1,C(1,2).
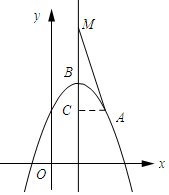
∵M(1,m),C(1,2),
∴MC=m-2.
∴cot∠AMB=
=m-2.
(3)∵抛物线的顶点坐标为(1,3),平移后抛物线的顶点坐标在x轴上,
∴抛物线向下平移了3个单位.
∴平移后抛物线的解析式为y=-x2+2x-1,PQ=3.
∵OP=OQ,
∴点O在PQ的垂直平分线上.
又∵QP∥y轴,
∴点Q与点P关于x轴对称.
∴点Q的纵坐标为-
.
将y=-
代入y=-x2+2x-1得:-x2+2x-1=-
,解得:x=
或x=
.
∴点Q的坐标为(
,-
)或(
,-
).
∴x=-
| b |
| 2a |
| -b |
| 2×(-1) |
∴y=-x2+2x+c.
将A(2,2)代入得:-4+4+c=2,解得:c=2.
∴抛物线的解析式为y=-x2+2x+2.
配方得:y=-(x-1)2+3.
∴抛物线的顶点坐标为(1,3).
(2)如图所示:过点A作AC⊥BM,垂足为C,则AC=1,C(1,2).

∵M(1,m),C(1,2),
∴MC=m-2.
∴cot∠AMB=
| CM |
| AC |
(3)∵抛物线的顶点坐标为(1,3),平移后抛物线的顶点坐标在x轴上,
∴抛物线向下平移了3个单位.
∴平移后抛物线的解析式为y=-x2+2x-1,PQ=3.
∵OP=OQ,
∴点O在PQ的垂直平分线上.
又∵QP∥y轴,
∴点Q与点P关于x轴对称.
∴点Q的纵坐标为-
| 3 |
| 2 |
将y=-
| 3 |
| 2 |
| 3 |
| 2 |
2+
| ||
| 2 |
2-
| ||
| 2 |
∴点Q的坐标为(
2+
| ||
| 2 |
| 3 |
| 2 |
2-
| ||
| 2 |
| 3 |
| 2 |
看了 已知在平面直角坐标系xOy中...的网友还看了以下:
初四二次函数:若二次函数y=ax^2+bx+c的图像经过点A(1,-3),定点为M,且方程ax^2 2020-05-15 …
如图,抛物线y=-x^2+bx+c经过点A(1,0)和点B(0,5).(1)求此抛物线的解析式及顶 2020-05-16 …
1.已知二次函数的图像经过原点及点(-1/2,-1/4),且图像与x轴的另一交点到原点的距离为1, 2020-05-16 …
已知抛物线y=ax2+bx+c经过A(1,0),B(3,0)C(0,3)三点.27.已知抛物线y= 2020-05-19 …
已知抛物线y=x2+bx+c(b、c为常数)1.若点(-1,0)和(-2,-2)在抛物线上2.若直 2020-06-06 …
(2014•长春)如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为 2020-07-22 …
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1)的抛物线y=ax²+bx+c(a 2020-07-29 …
已知二次函数y=ax2+bx+2,它的图象经过点(1,2).(1)若该图象与x轴的一个交点为(-1, 2020-12-08 …
根据下列条件,求出二次函数的解析式(1)抛物线y=ax2+bx+c经过点(0,1),(1,3),(- 2020-12-08 …
已知函数y=-ax^2+bx+c的图像过点P(-1,2)和Q(2,4)(1)证明:无论a为任何已知函 2020-12-23 …