早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系xOy中,函数y=ax2+bx+1(a≠0)的图象与x的正半轴交于点A,与x的负半轴交于点B,与y轴交于点C.△PAC中,P(1,-1),∠P=90°,PA=PC.(1)求点A的坐标.(2)将△PAC沿A
题目详情
如图,在平面直角坐标系xOy中,函数y=ax2+bx+1(a≠0)的图象与x的正半轴交于点A,与x的负半轴交于点B,与y轴交于点C.△PAC中,P(1,-1),∠P=90°,PA=PC.
(1)求点A的坐标.
(2)将△PAC沿AC翻折,若点P的对应点Q恰好落在函数y=ax2+bx+1(a≠0)的图象上,求a与b的值.
(3)将△ACO绕点A逆时针旋转90°得到△ADE,在x轴上取一点M,将∠PMD沿PM翻折,若点D的对应点F恰好落在x轴上,求点M的坐标.
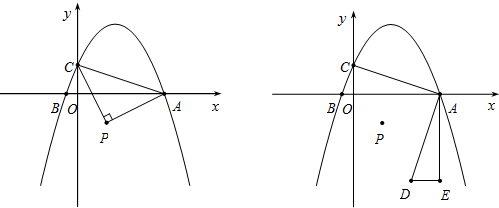
(1)求点A的坐标.
(2)将△PAC沿AC翻折,若点P的对应点Q恰好落在函数y=ax2+bx+1(a≠0)的图象上,求a与b的值.
(3)将△ACO绕点A逆时针旋转90°得到△ADE,在x轴上取一点M,将∠PMD沿PM翻折,若点D的对应点F恰好落在x轴上,求点M的坐标.
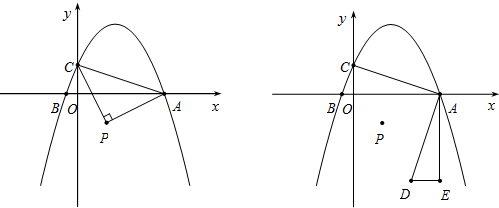
▼优质解答
答案和解析
(1)设点A的坐标为(a,0),
∵y=ax2+bx+1,
∴C(0,1),
∵P(1,-1),PA=PC,
∴
=
,
∴a=3或a=-1,
∴点A的坐标为(3,0);
(2)设直线AC的解析式为y=kx+b,
则
,
解得k=-
,b=1,
∴直线AC的解析式为y=-
x+1,
设点Q的坐标为(m,n),
∵点Q和点P关于直线AC对称轴,
∴Q(2,2),
∴
,
解得a=-
,b=
;
(3) D(2,-3),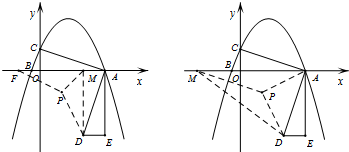
设点M(m,0),
由PD=PF得,F(-1,0)或F(3,0),
当点F(-1,0)时,由MD=MF得,(m-2)2+32=(m+1)2,解得m=2,
当点F(3,0)时,由MD=MF得,(m-2)2+32=(m-3)2,解得m=-2,
因此点M的坐标为(2,0)或(-2,0).
∵y=ax2+bx+1,
∴C(0,1),
∵P(1,-1),PA=PC,
∴
| 1+(-1-1)2 |
| (a-1)2+1 |
∴a=3或a=-1,
∴点A的坐标为(3,0);
(2)设直线AC的解析式为y=kx+b,
则
|
解得k=-
| 1 |
| 3 |
∴直线AC的解析式为y=-
| 1 |
| 3 |
设点Q的坐标为(m,n),
∵点Q和点P关于直线AC对称轴,
∴Q(2,2),
∴
|
解得a=-
| 5 |
| 6 |
| 13 |
| 6 |
(3) D(2,-3),

设点M(m,0),
由PD=PF得,F(-1,0)或F(3,0),
当点F(-1,0)时,由MD=MF得,(m-2)2+32=(m+1)2,解得m=2,
当点F(3,0)时,由MD=MF得,(m-2)2+32=(m-3)2,解得m=-2,
因此点M的坐标为(2,0)或(-2,0).
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
已知角a的顶点是坐标原点始边为X轴的正半轴,若P(4,y)已知角α的顶点为坐标原点,始边为x轴的正 2020-05-16 …
A(-4,0);B(2,4)①求线段AB与y轴的交点点C的坐标.②点P在X轴,S△ABP=20,求 2020-06-14 …
12、已知点P(-3,1)则P点关于x轴对称的点的坐标为;P点关于y轴对称的点的坐标为;P点关于原 2020-07-09 …
已知平面直角坐标系xOy,以O为极点,x轴的非负半轴为极轴建立极坐标系,P点的极坐标为,曲线C的极 2020-07-19 …
直线l的解析式为Y=3/4X+8,与x轴、y轴分别交于A、B两点,P是x轴上一点,以P为圆心的圆与 2020-07-20 …
以点M(-3,0)为圆心,5为半径画圆,分别交x轴的正半轴,负半轴于P,Q两点,则点p的坐标为一, 2020-07-26 …
已知曲线的直角坐标方程为.以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.P是曲线上一点,,, 2020-07-31 …
选修4-4:坐标系与参数方程已知极坐标系和直角坐标系中极点与坐标原点重合,极轴与x轴半轴重合,点P 2020-08-02 …
有一个带正电的金属球壳(厚度不计),其截面图如图a所示,O为球心,球壳P处开有半径远小于球半径的小孔 2021-01-09 …
一道中考数学题在平面直角坐标系内,A(-3,0),B在Y轴上方,角BAO=30度.P(3,0)绕o点 2021-01-22 …