早教吧作业答案频道 -->数学-->
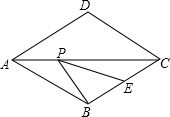
如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为.
题目详情
如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为___.

▼优质解答
答案和解析
连结DE.
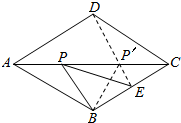 ∵BE的长度固定,
∵BE的长度固定,
∴要使△PBE的周长最小只需要PB+PE的长度最小即可,
∵四边形ABCD是菱形,
∴AC与BD互相垂直平分,
∴P′D=P′B,
∴PB+PE的最小长度为DE的长,
∵菱形ABCD的边长为4,E为BC的中点,∠DAB=60°,
∴△BCD是等边三角形,
又∵菱形ABCD的边长为4,
∴BD=4,BE=2,DE=2
,
∴△PBE的最小周长=DE+BE=2
+2,
故答案为:2
+2.
 ∵BE的长度固定,
∵BE的长度固定,∴要使△PBE的周长最小只需要PB+PE的长度最小即可,
∵四边形ABCD是菱形,
∴AC与BD互相垂直平分,
∴P′D=P′B,
∴PB+PE的最小长度为DE的长,
∵菱形ABCD的边长为4,E为BC的中点,∠DAB=60°,
∴△BCD是等边三角形,
又∵菱形ABCD的边长为4,
∴BD=4,BE=2,DE=2
| 3 |
∴△PBE的最小周长=DE+BE=2
| 3 |
故答案为:2
| 3 |
看了 如图,菱形ABCD的边长为4...的网友还看了以下:
E-R图是表示概念模型的有效工具之一,E-R图中使用菱形框表示()。A.联系B.实体C.实体的属性D 2020-05-24 …
ER图是表示概念模型的有效工具之一,ER图中使用菱形框表示________。A.联系B.实体C.实体 2020-05-24 …
E-R图是表示概念模型的有效工具之一,E-R图中使用菱形框表示A.联系B.实体C.实体的属性D.联系 2020-05-24 …
E-R图是表示概念模型的有效工具之一,E-R图中使用菱形框表示()。A.实体B.联系C.实体的属性D 2020-05-24 …
E-R图是表示概念模型的有效工具之一,E-R图中使用菱形框表示______。A.联系B.实体C.实体 2020-05-24 …
如图,把一些相同的菱形,按如图的方式排列,就构成一些大小不同的菱形,其中第一个图形中有3个菱形,第 2020-07-06 …
下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,按照图 2020-07-06 …
一个菱形的题目已知菱形ABCD,AC=16cm,BD=12cm,E、F、G、H是菱形各边的中点,求 2020-07-06 …
下列句中成语使用不正确的一项是()A.《香菱学诗》中,香菱孜孜不倦的学习精神一直为读者所称道.B. 2020-07-08 …
找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形 2020-07-15 …