早教吧作业答案频道 -->数学-->
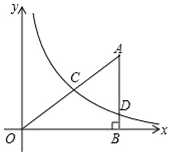
如图,在平面直角坐标系中,O为坐标原点,Rt△ABO的边AB垂直于x轴,垂足为点B,反比例函数y1=k1x(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AB=3.(1)求反比例函数y1=k1x(x>0
题目详情
如图,在平面直角坐标系中,O为坐标原点,Rt△ABO的边AB垂直于x轴,垂足为点B,反比例函数y1=
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AB=3.
(1)求反比例函数y1=
(x>0)的解析式;
(2)设经过C,D两点的一次函数解析式为y2=k2x+b,求出其解析式,并根据图象直接写出在第一象限内,当y2>y1时,x的取值范围.
| k1 |
| x |

(1)求反比例函数y1=
| k1 |
| x |
(2)设经过C,D两点的一次函数解析式为y2=k2x+b,求出其解析式,并根据图象直接写出在第一象限内,当y2>y1时,x的取值范围.
▼优质解答
答案和解析
(1)∵OB=4,AB=3,点A在第一象限,
∴点A的坐标为(4,3),
∵点C为线段OA的中点,
∴点C的坐标为(2,
).
∵点C在反比例函数y1=
(x>0)的图象上,
∴k1=2×
=3.
∴反比例函数的解析式为y=
(x>0).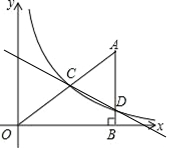
(2)当x=4时,y=
,
∴点D的坐标为(4,
).
将C(2,
)、B(4,
)代入y2=k2x+b,
,解得:
,
∴一次函数解析式为y2=-
x+
.
观察函数图象可知:当2<x<4时,一次函数图象在反比例函数图象的上方,
∴当y2>y1时,x的取值范围为2<x<4.
∴点A的坐标为(4,3),
∵点C为线段OA的中点,
∴点C的坐标为(2,
| 3 |
| 2 |
∵点C在反比例函数y1=
| k1 |
| x |
∴k1=2×
| 3 |
| 2 |
∴反比例函数的解析式为y=
| 3 |
| x |

(2)当x=4时,y=
| 3 |
| 4 |
∴点D的坐标为(4,
| 3 |
| 4 |
将C(2,
| 3 |
| 2 |
| 3 |
| 4 |
|
|
∴一次函数解析式为y2=-
| 3 |
| 8 |
| 9 |
| 4 |
观察函数图象可知:当2<x<4时,一次函数图象在反比例函数图象的上方,
∴当y2>y1时,x的取值范围为2<x<4.
看了 如图,在平面直角坐标系中,O...的网友还看了以下:
已知函数f(x)=√2/2(sinx+cosx)+3(x∈R)在等差数列{an}中,公差为d,其前 2020-04-26 …
有关反函数的!在线等…………………………一、解答题.1.求下列函数的反函数并画出原函数与它反函数的 2020-04-27 …
设直线l的方程为(a+1)x+y-2-a=0(x∈R)若直线l在两坐标轴上的截距相等,求l方程.: 2020-05-16 …
懂的来.1.已知f(n)=sin(n/3)π(n∈正整数),则f(1)+f(2)+f(3)+... 2020-06-12 …
Ⅰ:碱存在下,卤代烃与醇反应生成醚(R-O-R′):R-X+R′OHKOH/室温R-O-R′+HX 2020-07-15 …
在△ABC中,角A,B,C所对的边分别为a,b,c,函数f(x)=2cosxsin(x-A)+si 2020-07-26 …
已知函数f(x)=12(x+ax),(x≠0,x∈R)在(1,+∞)上为增函数,函数g(x)=ln 2020-08-01 …
文科函数,急1函数f(x)=x^3-a^x-1,若f(x)在实数集R上单调递增,求实数a的取值范围? 2020-11-21 …
(2014•天津)已知函数f(x)=3sinωx+cosωx(ω>0),x∈R,在曲线y=f(x)与 2020-11-25 …
设函数f(x)=a*2^x-1/2^x+1是在R上的奇函数已知函数f(x)=(a·2^x-1)/(2 2020-12-08 …