早教吧作业答案频道 -->数学-->
如图,在▱ABCD中,AB=2,BC=4,∠ABC=60°,E,F分别是BC,AD上的两点,且BE=DF,连AE,BF,DE,CF分别交于点G,H.(1)求证:四边形GEHF是平行四边形.(2)若E,F分别是BC,AD上的两个动点,设B
题目详情
如图,在▱ABCD中,AB=2,BC=4,∠ABC=60°,E,F分别是BC,AD上的两点,且BE=DF,连AE,BF,DE,CF分别交于点G,H.
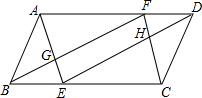
(1)求证:四边形GEHF是平行四边形.
(2)若E,F分别是BC,AD上的两个动点,设BE=DF=x,试推断当x等于多少时,四边形GEHF是矩形.

(1)求证:四边形GEHF是平行四边形.
(2)若E,F分别是BC,AD上的两个动点,设BE=DF=x,试推断当x等于多少时,四边形GEHF是矩形.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴BE∥DF,
∵BE=DF,
∴四边形FBED是平行四边形,
∴BF∥ED,即GF∥EH,
同理:四边形AECF是平行四边形,
∴AE∥FC,
即GE∥FH,
∴四边形GEHF是平行四边形;
(2) 当AE平分∠BAD,CF平分∠BCD时,BE=DF=2,四边形GEHF是矩形;理由如下:
∵四边形ABCD是平行四边形,
∴∠BAD=180°-∠ABC=180°-60°=120°,
∴∠ABC=∠BAC=∠AEB=60°,
∴△ABE是等边三角形,
∴BE=DF=AB=2,
∴AF=CE=BC-BE=4-2=2,
∴AB=AF,
∴∠ABG=∠AFG=30°,
∴∠AGB=90°,
∴∠EGF=90°,
∴四边形GEHF是矩形;
即当x=2时,四边形GEHF是矩形.
∴AD∥BC,AD=BC,
∴BE∥DF,
∵BE=DF,
∴四边形FBED是平行四边形,
∴BF∥ED,即GF∥EH,
同理:四边形AECF是平行四边形,
∴AE∥FC,
即GE∥FH,
∴四边形GEHF是平行四边形;
(2) 当AE平分∠BAD,CF平分∠BCD时,BE=DF=2,四边形GEHF是矩形;理由如下:
∵四边形ABCD是平行四边形,
∴∠BAD=180°-∠ABC=180°-60°=120°,
∴∠ABC=∠BAC=∠AEB=60°,
∴△ABE是等边三角形,
∴BE=DF=AB=2,
∴AF=CE=BC-BE=4-2=2,
∴AB=AF,
∴∠ABG=∠AFG=30°,
∴∠AGB=90°,
∴∠EGF=90°,
∴四边形GEHF是矩形;
即当x=2时,四边形GEHF是矩形.
看了 如图,在▱ABCD中,AB=...的网友还看了以下:
在三角形ABC中,AD垂直BC于D,过D做DE垂直AC于E,过D做DF垂直AB于F,求证:B,C, 2020-05-21 …
在以下认证方式中,最常用的认证方式是______。A.基于账户名口令认证B.基于摘要算法认证C. 基 2020-05-23 …
在以下认证方式中,最常用的认证方式是______。A.基于账户名/口令认证B.基于摘要算法认证C.基 2020-05-23 …
在以下认证方式中,最常用的认证方式是 ______。A.基于账户名/口令认证B.基于摘要算法认证C. 2020-05-24 …
在以下认证方式中,最常用的认证方式是A.基于账户名/口令认证B.基于摘要算法认证C.基于PKI认证D 2020-05-24 …
在以下认证方式中,最常用的认证方式是A.基于账户名/口令认证B.基于摘要算法认证C.基于 PKI 认 2020-05-24 …
面向身份信息的认证应用中,最常用的认证方式是( )。A.基于数据库认证B.基于摘要算法认证C.基于P 2020-05-26 …
已知a+b+c=0,abc不等于0,且a,b,c,互不相等,求证:[(b-c)/a+(c-a)/b+ 2020-12-01 …
已知a+b+c=0,abc不等于0,且a,b,c,互不相等,求证:[(b-c)/a+(c-a)/b+ 2020-12-01 …
已知二次函数y=ax平方+bx+c,(1)若a=2,b+c=-2,b>c,且二次函数的图像经过点(p 2020-12-08 …