早教吧作业答案频道 -->数学-->
已知函数f（x）=x2+4x，x≤0xlnx，x>0，g（x）=kx-1，若函数y=f（x）-g（x）有且仅有4个不同的零点．则实数k的取值范围为（）A.（1，6）B.（0，1）C.（1，2）D.（2，+∞）
题目详情
已知函数f（x）=
，g（x）=kx-1，若函数y=f（x）-g（x）有且仅有4个不同的零点．则实数k的取值范围为（ ）x2+4x，x≤0 xlnx，x>0
A. （1，6）
B. （0，1）
C. （1，2）
D. （2，+∞）
▼优质解答
答案和解析
∵函数y=f（x）-g（x）有且仅有4个不同的零点，
∴函数f（x）=
与g（x）=kx-1的图象有四个不同的交点，
作函数f（x）=
与g（x）=kx-1的图象如下，
，
易知直线y=kx-1恒过点（0，-1）；
设A（x，x2+4x），y′=2x+4；
故2x+4=
，
故x=-1；
故k=-2+4=2；
设B（x，xlnx），y′=lnx+1，
则lnx+1=
，
解得，x=1，故k=ln1+1=1，
结合图象可知，
实数k的取值范围为（1，2），
故选C．
∴函数f（x）=
|
作函数f（x）=
|
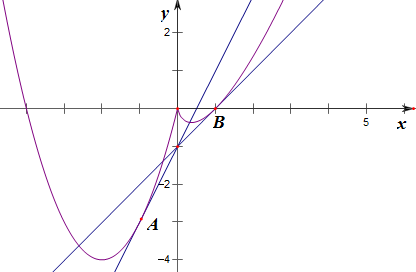，易知直线y=kx-1恒过点（0，-1）；
设A（x，x2+4x），y′=2x+4；
故2x+4=
| x2+4x+1 |
| x |
故x=-1；
故k=-2+4=2；
设B（x，xlnx），y′=lnx+1，
则lnx+1=
| xlnx+1 |
| x |
解得，x=1，故k=ln1+1=1，
结合图象可知，
实数k的取值范围为（1，2），
故选C．
看了 已知函数f（x）=x2+4x...的网友还看了以下：
数学什么判断一个点是否在圆内（求三种2种圆的表达式时的判断方法,----基本式与 X^2+Y^=R 2020-05-16 …
线性规划数学题：实数x,y满足x-y+1≤0,x>0,y≤2,若实数x,y满足x-y+1≤0,x> 2020-05-16 …
规定一种新的运算：x※y=x·y-x+y,若2※x=4,求x的值.明天就要! 2020-05-22 …
规定一种新的运算：x※y=x·y-x+y,若2※x=4,求x的值.明天就要! 2020-05-22 …
已知函数f(x)=x3+ax2+bx若函数f(x)在x=2处有极值-6,求y=(x)的单调递减区间 2020-06-27 …
构造方程若实数x,y满足x/3的三次方+4的三次方+y/3的三次方+6的三次方=1,x/5的三次方 2020-07-16 …
x^2+y^2=133^2+（4-x）^2=2^2+（6-y）^2数学请给过程解方程 2020-07-17 …
若|X-3|+(2X-Y-K)^2=0,Y是非负数,求K的取值范围?(1)当Y是非正数,K的取值范 2020-08-03 …
若2x+3y-1=y-x-8=x+6,则2x-y=()若2分之3x-4y=-1,则代数式8y=6x+ 2020-10-31 …
x为全体实数,函数y=x^(2/2)写成根式的形式应该是y=√(x^2)还是y=(√x)^2,数学里 2020-11-07 …