早教吧作业答案频道 -->数学-->
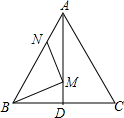
如图,在等边△ABC中,AB=4,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是.
题目详情
如图,在等边△ABC中,AB=4,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是___.

▼优质解答
答案和解析
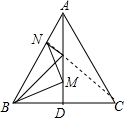 过C作CN⊥AB于N,交AD于M,连接BM,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BM+MN=CN,
过C作CN⊥AB于N,交AD于M,连接BM,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BM+MN=CN,
∵等边△ABC中,AD平分∠CAB,
∴AD⊥BC,
∴AD是BC的垂直平分线(三线合一),
∴C和B关于直线AD对称,
∴CM=BM,
即BM+MN=CM+MN=CN,
∵CN⊥AB,
∴∠CNB=90°,CN是∠ACB的平分线,AN=BN(三线合一),
∵∠ACB=60°,
∴∠BCN=30°,
∵AB=4,
∴BN=
AB=2,
在△BCN中,由勾股定理得:CN=
=
=2
,即BM+MN的最小值是2
.
故答案为:2
.
 过C作CN⊥AB于N,交AD于M,连接BM,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BM+MN=CN,
过C作CN⊥AB于N,交AD于M,连接BM,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BM+MN=CN,∵等边△ABC中,AD平分∠CAB,
∴AD⊥BC,
∴AD是BC的垂直平分线(三线合一),
∴C和B关于直线AD对称,
∴CM=BM,
即BM+MN=CM+MN=CN,
∵CN⊥AB,
∴∠CNB=90°,CN是∠ACB的平分线,AN=BN(三线合一),
∵∠ACB=60°,
∴∠BCN=30°,
∵AB=4,
∴BN=
| 1 |
| 2 |
在△BCN中,由勾股定理得:CN=
| BC2-BN2 |
| 42-22 |
| 3 |
| 3 |
故答案为:2
| 3 |
看了 如图,在等边△ABC中,AB...的网友还看了以下:
问几个c问题1,设x=2.5,y=4.7,a=7,则x+a%3*(int)(x+y)%2/4=2, 2020-04-08 …
有下列命题:①“若a<b<0,则a2>ab>b2”②命题“a、b都是偶数,则a+b是偶数”的逆否命 2020-04-09 …
命题“若a,b都是奇数,则a-b是偶数”的逆否命是()A.若a-b不是偶数,则a,b不都是奇数B. 2020-04-09 …
1、绝对值小于二又三分之一的整数分别是什么2、|a|=|b|,a=5,则b的值等于多少3、若-m= 2020-04-09 …
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
设l,m是两条不同的直线,a是一个平面,有下列四个命题:(1)若l⊥a,m⊂a,则l⊥m;(2)若 2020-05-13 …
1.设m,n是两条不同的直线,a,b,c是三个不同的平面,则下列正确的是A.若a//c,b//c, 2020-05-13 …
设A与B均为N阶矩阵,则下列结论正确的是:A若/AB/=0则A=0或B=0B若/AB/=0,则/A 2020-05-14 …
若关于x的分式方程(x-a)/(x-1) -3/x=1无解,则a=两边乘x(x-1)x(x-a)- 2020-05-15 …
下列变形错误的是.a.若a=b,则a-3=b-3b.若a=b,则7a-1=7b-1c.若a=b,则 2020-06-06 …