早教吧作业答案频道 -->数学-->
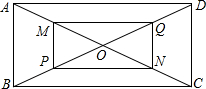
已知：如图，在矩形ABCD中，对角线AC与BD相交于点O，点M，P，N，Q分别在AO，BO，CO，DC上，且AM=BP=CN=DQ．求证：四边形MPNQ是矩形．
题目详情
已知：如图，在矩形ABCD中，对角线AC与BD相交于点O，点M，P，N，Q分别在AO，BO，CO，DC上，且AM=BP=CN=DQ．求证：四边形MPNQ是矩形．
▼优质解答
答案和解析
∵四边形ABCD是矩形，
∴∠ABC=90°；AC=BD，AO=
AC，BO=
BD；
∴AO=BO；而AM=BP，
∴AM：AO=BP：BO，
∴MP∥AB；同理可证：QN∥CD；
∵AB∥CD，
∴MP∥QN；同理可证：MQ∥PN，
∴四边形MPNQ是平行四边形；
∵MP∥AB，PN∥BC，∠ABC=90°，
∴∠MPN=90°，
∴四边形MPNQ是矩形．
∴∠ABC=90°；AC=BD，AO=
| 1 |
| 2 |
| 1 |
| 2 |
∴AO=BO；而AM=BP，
∴AM：AO=BP：BO，
∴MP∥AB；同理可证：QN∥CD；
∵AB∥CD，
∴MP∥QN；同理可证：MQ∥PN，
∴四边形MPNQ是平行四边形；
∵MP∥AB，PN∥BC，∠ABC=90°，
∴∠MPN=90°，
∴四边形MPNQ是矩形．
看了 已知：如图，在矩形ABCD中...的网友还看了以下：
已知an=2n,令bn=λq^(an)+λ(λ,q为常数,q>0且q≠1),Cn=3+n+(b1+ 2020-04-27 …
数列{an}是以a为着项，q为公比的等比数列，令bn=1-a1-a2-a3-…-an，Cn=2-b 2020-05-13 …
关于微分的几何意义,通常看到这样的表达:"设Δx是曲线y = f(x)上的点M的在横坐标上的增量, 2020-05-16 …
数学排列组合题!作对就采纳!1.求证Cn+2^m=Cn^m+2Cn^m-1+Cn^m-22.（1） 2020-07-01 …
如图，正方形ABCD中，M为AD边上的一点，连接BM，过点C作CN∥BM，交AD的延长线于点N，在 2020-07-07 …
如图1，在△ABC中，∠B=60°，点M从点B出发沿射线BC方向，在射线BC上运动．在点M运动的过 2020-07-27 …
在f(m,n)中,.m.n.f(m,n)均为非负整数且对任意的m,n有f(0,n)=n+1,f(m 2020-07-31 …
一道求证题（与二项式定理有关）C10(0)*C20(20)+C10(1)*C20(1)+…+C10( 2020-10-31 …
二项式的有关..已知组合数Cn^m对任意的有意义的m都成立,求n的值要能听懂的躲不起啊我写错啦题；C 2020-11-07 …
已知数列{an}的前n项和为Sn,且满足Sn=2an-n若bn=log2(an+1),在bk(k为下 2020-11-19 …