早教吧作业答案频道 -->数学-->
已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于
题目详情
已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点.
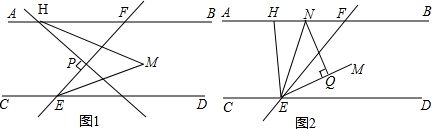
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.

(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.
▼优质解答
答案和解析
(1)如图1,作MQ∥AB,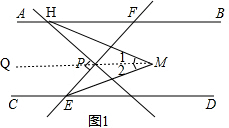 ,
,
∵AB∥CD,MQ∥AB,
∴MQ∥CD,
∴∠1=∠FHM,∠2=∠DEM,
∴∠1+∠2=∠FHM+∠DEM=
(∠FHP+∠FED)=
(∠FHP+∠HFP),
∵HP⊥EF,
∴∠HPF=90°,
∴∠FHP+∠HFP=180°-90°=90°,
∵∠1+∠2=∠M,
∴∠M=
×90°=45°.
(2)①如图2,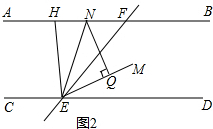 ,
,
∠FHE=2∠ENQ,理由如下:
∠NEQ=∠NEF+∠QEF=
(∠HEF+∠DEF)=
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=
(180°-∠HED)=
∠CEH,
∵AB∥CD,
∴∠FHE=∠CEH=2∠ENQ.
②如图3,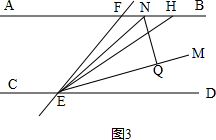 ,
,
∠FHE=180°-2∠ENQ,理由如下:
∠NEQ=∠QEF-∠NEF=
(∠DEF-∠HEF)=
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=
(180°-∠HED)=
∠CEH,
∵AB∥CD,
∴∠FHE=180°-∠CEH=180°-2∠ENQ.
综上,可得
当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°-2∠ENQ.
 ,
,∵AB∥CD,MQ∥AB,
∴MQ∥CD,
∴∠1=∠FHM,∠2=∠DEM,
∴∠1+∠2=∠FHM+∠DEM=
| 1 |
| 2 |
| 1 |
| 2 |
∵HP⊥EF,
∴∠HPF=90°,
∴∠FHP+∠HFP=180°-90°=90°,
∵∠1+∠2=∠M,
∴∠M=
| 1 |
| 2 |
(2)①如图2,
 ,
,∠FHE=2∠ENQ,理由如下:
∠NEQ=∠NEF+∠QEF=
| 1 |
| 2 |
| 1 |
| 2 |
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴∠FHE=∠CEH=2∠ENQ.
②如图3,
 ,
,∠FHE=180°-2∠ENQ,理由如下:
∠NEQ=∠QEF-∠NEF=
| 1 |
| 2 |
| 1 |
| 2 |
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴∠FHE=180°-∠CEH=180°-2∠ENQ.
综上,可得
当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°-2∠ENQ.
看了 已知:直线EF分别与直线AB...的网友还看了以下:
求斜线段的中点,如(1,-2),(1,-5)的中点,是不是(5-2)除2,写出道理,忘了,是平面直 2020-06-08 …
探索新知如图1,点C将线段AB分成AC和BC两部分,若BC=πAC,则称点C是线段AB的圆周率点, 2020-06-14 …
六年级十七课松鼠的问题!1、2段分别从什么角度说明松鼠乖巧的特点的?1段:2段:用简明的概括第3段 2020-06-20 …
如图,点o是线段ab的中点,AB=24cm.(1)如果M,N亮点把线段AB分成1:4:3三部分,求 2020-07-25 …
如图,点o是线段ab的中点,AB=24cm.(1)如果M,N亮点把线段AB分成1:4:3三部分,求 2020-07-25 …
一至一百的π值详细一点如:1*3.14=3.142*3.14=2.68 2020-07-26 …
一条直线从左到右顺次排列着1987个点:P1P2~P1987,已知点PK是线段PK-1PK+1的K 2020-08-02 …
①线段AB内有一点M,1,如果AM=BM,那么,点M是AB的;2如果AM=1/2AB,那么,点M是A 2020-11-07 …
举例说明各种信息传播方式的优点和缺点要举例子常用的例子一般是说电视电脑的优缺点举例说明各种信息传播方 2020-11-27 …
数学找规律题线段AB上的点数包括端点与线段的总数有如下关系:如果线段上有2个点时,可以确定1条线段; 2020-11-27 …