早教吧作业答案频道 -->数学-->
如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作O交AC于点D,交BE于点F.(1)求证:BC是O的切线;(2)若AB=8,BC=6,求DE的长.
题目详情
如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作 O交AC于点D,交BE于点F.
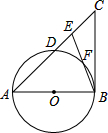
(1)求证:BC是 O的切线;
(2)若AB=8,BC=6,求DE的长.

(1)求证:BC是 O的切线;
(2)若AB=8,BC=6,求DE的长.
▼优质解答
答案和解析
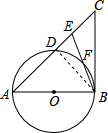 (1)证明:∵AE=AB,
(1)证明:∵AE=AB,
∴△ABE是等腰三角形,
∴∠ABE=
(180°-∠BAC=)=90°-
∠BAC,
∵∠BAC=2∠CBE,
∴∠CBE=
∠BAC,
∴∠ABC=∠ABE+∠CBE=(90°-
∠BAC)+
∠BAC=90°,
即AB⊥BC,
∴BC是 O的切线;
(2) 连接BD,
∵AB是 O的直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABD∽△ACB,
∴
=
,
∵在Rt△ABC中,AB=8,BC=6,
∴AC=
=10,
∴
=
,
解得:AD=6.4,
∵AE=AB=8,
∴DE=AE-AD=8-6.4=1.6.
 (1)证明:∵AE=AB,
(1)证明:∵AE=AB,∴△ABE是等腰三角形,
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BAC=2∠CBE,
∴∠CBE=
| 1 |
| 2 |
∴∠ABC=∠ABE+∠CBE=(90°-
| 1 |
| 2 |
| 1 |
| 2 |
即AB⊥BC,
∴BC是 O的切线;
(2) 连接BD,
∵AB是 O的直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABD∽△ACB,
∴
| AD |
| AB |
| AB |
| AC |
∵在Rt△ABC中,AB=8,BC=6,
∴AC=
| AB2+BC2 |
∴
| AD |
| 8 |
| 8 |
| 10 |
解得:AD=6.4,
∵AE=AB=8,
∴DE=AE-AD=8-6.4=1.6.
看了 如图,在△ABC中,E是AC...的网友还看了以下:
怎样变换公式?例如圆周长的公式:C=2πr如何变换成r=C/(2π)教教我具体方法吧,为什么要同时 2020-04-12 …
已知三角形的三个顶点分别为A(6,-7),B(-2,3),C(2,1),求AC边上的中线所在的直线 2020-06-03 …
在△ABC中,已知sin[B+(C/2)]=4/5,求cos(A-B)的值.过程中有一步不懂,co 2020-06-03 …
1.如图,在△ABC中,AB=2cm,AC=3cm,BC=4cm,AD平分∠BAC交BC于D.则B 2020-06-05 …
直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;(2)如果a∥b,b∥c,那么a∥ 2020-11-02 …
如果实数a,b,c满足a2+b2+c2=9,那么代数式(a-b)2+(b-c)2+(c-a)2的最大 2020-11-18 …
有理数a、b、c在数轴上的位置如图所示,试简化|a+b|-|b-2|-|a-c|-|2-c|图发不上 2020-11-20 …
有关集合的问题A={c,15,a,1,2{1,2},3,4,Φ},B={e,j,1,2,{1,c,2 2020-11-23 …
有关化学系统命名法c-c-c-c-c-c-c||cc-c如何命名~主链从哪边编号?上面的式子因为空格 2020-11-24 …
已知二次函数y=ax平方+bx+c,(1)若a=2,b+c=-2,b>c,且二次函数的图像经过点(p 2020-12-08 …