早教吧作业答案频道 -->数学-->
在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.(1)如图1,若点F与点A重合,求证:AC=BC;(2)若∠DAF=∠DBA,①如图2,当点F在线
题目详情
在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
(1)如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
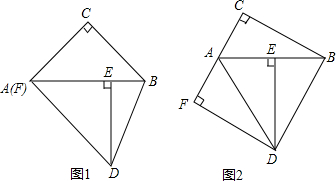
(1)如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.

▼优质解答
答案和解析
(1)由旋转得,∠BAC=∠BAD,
∵DF⊥AC,
∴∠CAD=90°,
∴∠BAC=∠BAD=45°,
∵∠ACB=90°,
∴∠ABC=45°,
∴AC=CB,
(2)①由旋转得,AD=AB,
∴∠ABD=∠ADB,
∵∠DAF=∠ABD,
∴∠DAF=∠ADB,
∴AF∥BD,
∴∠BAC=∠ABD,
∵∠ABD=∠FAD
由旋转得,∠BAC=∠BAD,
∴∠FAD=∠BAC=∠BAD=
×180°=60°,
由旋转得,AB=AD,
∴△ABD是等边三角形,
∴AD=BD,
在△AFD和△BED中,
,
∴△AFD≌△BED,
∴AF=BE,
②如图,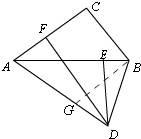
由旋转得,∠BAC=∠BAD,
∵∠ABD=∠FAD=∠BAC+∠BAD=2∠BAD,
由旋转得,AD=AB,
∴∠ABD=∠ADB=2∠BAD,
∵∠BAD+∠ABD+∠ADB=180°,
∴∠BAD+2∠BAD+2∠BAD=180°,
∴∠BAD=36°,
设BD=y,作BG平分∠ABD,
∴∠BAD=∠GBD=36°
∴AG=BG=BD=y,
∴DG=AD-AG=AD-BG=AD-BD,
∵∠BDG=∠ADB,
∴△BDG∽△ADB,
∴
=
.
∴
=
=
-1,即(
)2-
-1=0,
∴
=
,
∵∠FAD=∠EBD,∠AFD=∠BED,
∴△AFD∽△BED,
∴
=
,
∴AF=
×BE=
x.
∵DF⊥AC,
∴∠CAD=90°,
∴∠BAC=∠BAD=45°,
∵∠ACB=90°,
∴∠ABC=45°,
∴AC=CB,
(2)①由旋转得,AD=AB,
∴∠ABD=∠ADB,
∵∠DAF=∠ABD,
∴∠DAF=∠ADB,
∴AF∥BD,
∴∠BAC=∠ABD,
∵∠ABD=∠FAD
由旋转得,∠BAC=∠BAD,
∴∠FAD=∠BAC=∠BAD=
| 1 |
| 3 |
由旋转得,AB=AD,
∴△ABD是等边三角形,
∴AD=BD,
在△AFD和△BED中,
|
∴△AFD≌△BED,
∴AF=BE,
②如图,

由旋转得,∠BAC=∠BAD,
∵∠ABD=∠FAD=∠BAC+∠BAD=2∠BAD,
由旋转得,AD=AB,
∴∠ABD=∠ADB=2∠BAD,
∵∠BAD+∠ABD+∠ADB=180°,
∴∠BAD+2∠BAD+2∠BAD=180°,
∴∠BAD=36°,
设BD=y,作BG平分∠ABD,
∴∠BAD=∠GBD=36°
∴AG=BG=BD=y,
∴DG=AD-AG=AD-BG=AD-BD,
∵∠BDG=∠ADB,
∴△BDG∽△ADB,
∴
| BD |
| AD |
| DG |
| DB |
∴
| BD |
| AD |
| AD-BD |
| BD |
| AD |
| BD |
| AD |
| BD |
| AD |
| BD |
∴
| AD |
| BD |
1+
| ||
| 2 |
∵∠FAD=∠EBD,∠AFD=∠BED,
∴△AFD∽△BED,
∴
| AD |
| BD |
| AF |
| BE |
∴AF=
| AD |
| BD |
1+
| ||
| 2 |
看了 在Rt△ABC中,∠C=90...的网友还看了以下:
如图,E,F,G,H,分别为正方体ABCD—A1B1C1D1,的棱A1B1,A1D1,B1C1,D 2020-05-13 …
虽能帮我看看lingo程序哪里错了model:sets:a/1..3/:d;b/1..3/;c(a 2020-05-13 …
已知集合M={-3,-2,-1,0,1,2,},若a,b属于M,平面直角坐标系内点P的坐标是(a, 2020-05-16 …
互感器避雷器安装用支架接地应有()与接地网可靠连接。A.0 点B.1 点C.2 点D.3 点 2020-05-30 …
1,.如图1,已知△ABC是等边三角形,BD是高,延长BC到点E,使CE=CD,过点D作DF⊥BE 2020-06-03 …
用标准格式用这种:∵∴如果a,b,c,d互为不相等的有理数,且c=3,|a-c=|b-c|=|d- 2020-06-04 …
求解a(1/b+1/c+1/d)+b(1/a+1/c+1/d)+c(1/b+1/a+1/d)+d( 2020-06-12 …
在三角形abc中,A(1,0)B(5,O)C(2,3)点D是BC上的一点,且BD=2DC求点D的坐 2020-06-16 …
有一个二次函数的题目,请各位帮帮我~~~~如图,已知抛物线的顶点为点A(3,2),且经过原点o,与 2020-06-27 …
下图所示区域为地球某日的夜半球,A为圆心。读图回答此时北京时间是A.2点40分B.14点40分C. 2020-07-15 …