早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的
题目详情
如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A-B-C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.
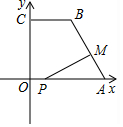
(1)求AB长;
(2)设△PAM的面积为S,当0≤t≤5时,求S与t的函数关系式,并指出S取最大值时,点P的位置;
(3)t为何值时,△APM为直角三角形?

(1)求AB长;
(2)设△PAM的面积为S,当0≤t≤5时,求S与t的函数关系式,并指出S取最大值时,点P的位置;
(3)t为何值时,△APM为直角三角形?
▼优质解答
答案和解析
(1)如图1,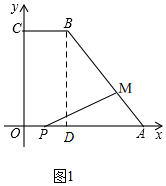 过点B作BD⊥x轴于点D,
过点B作BD⊥x轴于点D,
∵A(10,0),B(4,8)C(0,8),
∴AO=10,BD=8,AD=6,
由勾股定理可求得:AB=10,
(2)∵AB=10,
∴10÷2=5,
∵0≤t≤5,
∴点M在AB上,
作ME⊥OA于E,
∴△AEM∽△ADB,
∴
=
,
∴
=
,
∴ME=
t,
∴S=
PA•ME=
(10-t)•
t=-
t2+8t=-
(t-5)2+20,
∵0≤t≤5,
∴t=5时,S取最大值,此时PA=10-t=5,
即:点P在OA的中点处.
(3)由题意可知:0≤t≤7,
当点P是直角顶点时,
∴PM⊥AP,
∴PA=10-t,
若0≤t≤5时,点M在AB上,如图2,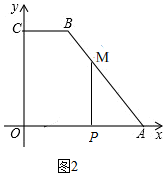
此时AM=2t,
∵cos∠BAO=
,
∴
=
,
∴
=
∴t=
,
若5<t≤7时,点M在BC上,如图3,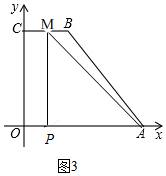
∴CM=14-2t,OP=t,
∴OP=CM,
∴t=14-2t,
∴t=
,
当点A是直角顶点时,
此时,∠MAP不可能为90°,此情况不符合题意;
当点M是直角顶点时,
若0≤t≤5时,M在AB上,如图4,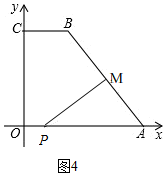
此时,AM=2t,AP=10-t
∵cos∠BAO=
,
∴
=
,
∴
=
,
∴t=
,
若5<t≤7时,点M在BC上,如图5,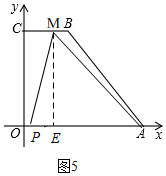
过点M作ME⊥x轴于点E,
此时,CM=14-2t,OP=t,
∴ME=8,PE=CM-OP=14-3t,
∴EA=10-(14-2t)=2t-4,
∵∠PMA=∠MEA=90°,
∴∠PME+∠EMA=∠EMA+∠MAP=90°,
∴∠PME=∠MAP,
∴△PME∽△MAE,
∴
=
,
∴ME2=PE•EA,
∴64=(14-3t)(2t-4),
∴3t2-8t+60=0,
△=-656<0,故此情况不存在;
综上所述,t=
或
 过点B作BD⊥x轴于点D,
过点B作BD⊥x轴于点D,∵A(10,0),B(4,8)C(0,8),
∴AO=10,BD=8,AD=6,
由勾股定理可求得:AB=10,
(2)∵AB=10,
∴10÷2=5,
∵0≤t≤5,
∴点M在AB上,
作ME⊥OA于E,
∴△AEM∽△ADB,
∴
| ME |
| BD |
| AM |
| AB |
∴
| ME |
| 8 |
| 2t |
| 10 |
∴ME=
| 8 |
| 5 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
∵0≤t≤5,
∴t=5时,S取最大值,此时PA=10-t=5,
即:点P在OA的中点处.
(3)由题意可知:0≤t≤7,
当点P是直角顶点时,
∴PM⊥AP,
∴PA=10-t,
若0≤t≤5时,点M在AB上,如图2,

此时AM=2t,
∵cos∠BAO=
| 3 |
| 5 |
∴
| AP |
| AM |
| 3 |
| 5 |
∴
| 10-t |
| 2t |
| 3 |
| 5 |
∴t=
| 50 |
| 11 |
若5<t≤7时,点M在BC上,如图3,

∴CM=14-2t,OP=t,
∴OP=CM,
∴t=14-2t,
∴t=
| 14 |
| 3 |
当点A是直角顶点时,
此时,∠MAP不可能为90°,此情况不符合题意;
当点M是直角顶点时,
若0≤t≤5时,M在AB上,如图4,

此时,AM=2t,AP=10-t
∵cos∠BAO=
| 3 |
| 5 |
∴
| AM |
| AP |
| 3 |
| 5 |
∴
| 2t |
| 10-t |
| 3 |
| 5 |
∴t=
| 30 |
| 13 |
若5<t≤7时,点M在BC上,如图5,

过点M作ME⊥x轴于点E,
此时,CM=14-2t,OP=t,
∴ME=8,PE=CM-OP=14-3t,
∴EA=10-(14-2t)=2t-4,
∵∠PMA=∠MEA=90°,
∴∠PME+∠EMA=∠EMA+∠MAP=90°,
∴∠PME=∠MAP,
∴△PME∽△MAE,
∴
| ME |
| PE |
| EA |
| ME |
∴ME2=PE•EA,
∴64=(14-3t)(2t-4),
∴3t2-8t+60=0,
△=-656<0,故此情况不存在;
综上所述,t=
| 50 |
| 11 |
看了 如图,在平面直角坐标系中,已...的网友还看了以下:
锥形圆柱形怎么算角度!例如!车床要车一头直径50mm另一头直径70mm长200MM锥形的圆柱体·该怎 2020-03-31 …
如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每 2020-04-22 …
如图,在三角形ABC中,角B=90度,角C=34度,角1=角2,角ADC=104度,如图,在三角形 2020-05-14 …
如图,在三角形ABC中,角ACB=90度,角ABC=30度,将三角形ABC绕点C按顺时针方向旋转角 2020-06-27 …
三角形ABc中与角C相邻的外角为100度,角A-角B=30度,则角A=度,角B=三角形ABc中与角 2020-07-09 …
三角形ABC中,角ABC,角ACB的平分线相交于点O(1)若角ABC=40度,角ACB=50度,则 2020-07-18 …
已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是(0,83) 2020-07-22 …
如图角1=60度,角2=120度,角3=60度.AC与BD有怎样的位置关系?为什么?AC与BD平行 2020-07-23 …
折射率的单位是角度还是弧度用分光仪测折射率,计算不确定度的时候用不用在将角度换成弧度来表示最后结果 2020-07-30 …
把质量m=0.2kg的石块从h=15m高处以30度角,斜向上抛出...把质量m=0.2kg的石块从h 2021-01-12 …
 扫描下载二维码
扫描下载二维码