早教吧作业答案频道 -->数学-->
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形,∠BAD=60°,P为AB的中点,Q为CD1的中点.(1)求证:DP⊥平面A1ABB1;(2)求证:PQ∥平面ADD1A1.(3)若E为CC1的中点,能否在CP上找一点F
题目详情
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形,∠BAD=60°,P为AB的中点,Q为CD1的中点.
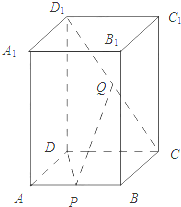
(1)求证:DP⊥平面A1ABB1;
(2)求证:PQ∥平面ADD1A1.
(3)若E为CC1的中点,能否在CP上找一点F,使得EF∥面DPQ?并给出证明过程.

(1)求证:DP⊥平面A1ABB1;
(2)求证:PQ∥平面ADD1A1.
(3)若E为CC1的中点,能否在CP上找一点F,使得EF∥面DPQ?并给出证明过程.
▼优质解答
答案和解析
证明:(1)连结BD
∵在四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,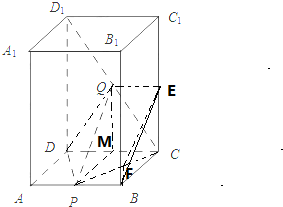
∴AP=AB=BD,
∵P为AB的中点,∴DP⊥AB,
∵AA1⊥平面ABCD,DP⊂平面ABCD,
∴AA1⊥DP,
∵AA1∩AB=A,∴DP⊥平面A1ABB1.
(2)取CD中点M,连结PM、QM,
∵P为AB的中点,Q为CD1的中点,
∴PM∥AD,QM∥DD1,
∵AD∩DD1=D,PM∩QM=M,
AD、DD1⊂平面ADD1,PM、QM⊂平面PQF,
∴平面ADD1∥平面MPQ,
∵PQ⊂平面PQF,∴PQ∥平面ADD1A1.
(3)连结EB,
∵Q为CD1的中点,E是CC1的中点,P为AB中点,∴QE
PB,
∴四边形PBEQ是平行四边形,∴BE∥PQ,
过B作BF∥AD,交PC于F,
∵BE∥PQ,BF∥AD,BE∩BF=B,PQ∩PD=P,
BE、BF⊂平面BEF,PQ、PD⊂平面PDQ,
∴平面BEF∥平面PDQ,
∵EF⊂平面BEF,∴EF∥面DPQ.
∵在四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,∠BAD=60°,

∴AP=AB=BD,
∵P为AB的中点,∴DP⊥AB,
∵AA1⊥平面ABCD,DP⊂平面ABCD,
∴AA1⊥DP,
∵AA1∩AB=A,∴DP⊥平面A1ABB1.
(2)取CD中点M,连结PM、QM,
∵P为AB的中点,Q为CD1的中点,
∴PM∥AD,QM∥DD1,
∵AD∩DD1=D,PM∩QM=M,
AD、DD1⊂平面ADD1,PM、QM⊂平面PQF,
∴平面ADD1∥平面MPQ,
∵PQ⊂平面PQF,∴PQ∥平面ADD1A1.
(3)连结EB,
∵Q为CD1的中点,E是CC1的中点,P为AB中点,∴QE
| ∥ |
. |
∴四边形PBEQ是平行四边形,∴BE∥PQ,
过B作BF∥AD,交PC于F,
∵BE∥PQ,BF∥AD,BE∩BF=B,PQ∩PD=P,
BE、BF⊂平面BEF,PQ、PD⊂平面PDQ,
∴平面BEF∥平面PDQ,
∵EF⊂平面BEF,∴EF∥面DPQ.
看了 在四棱柱ABCD-A1B1C...的网友还看了以下:
水平面上A,B,C三点固定着三个电荷量为Q的正点电荷,将另一个质量为m的带正电的小球(可视为点电荷 2020-05-13 …
1.已知平行四边形ABCD的三个顶点A,B,C的坐标分别为(-2,1),(-1,3),(3,4), 2020-05-13 …
如图,数轴上A,B,C,D四点对应的数都是整数若A对应的数为a,B对应的数为b,C对应的数为c,且 2020-05-15 …
★高二数学★椭圆c的中心在原点,左焦点F1,右焦点F2均在x轴上椭圆c的中心在原点,左焦点F1,右 2020-05-16 …
A与B有如下的反应:A+B生成C+D 若c为厨房内常用的调味品,在A溶液中加入铁粉能产生氢气,则A 2020-05-16 …
如下,我知道是D求为什么在没有标出原点的数轴上A,B,C,D四点对应的有理数都是整数.且其中一个位 2020-06-06 …
如图所示,三个同心圆是同一个点电荷周围的三个等势面,已知这三个圆的半径成等差数列.A、B、C分别是 2020-06-06 …
请你自己画图:画一个三角形ABC,三个顶点分别表上A,B,C.在BC边上任意取三个点(与B,C不重 2020-06-07 …
已知c=ma+nb=(-2倍根号3,2),a⊥c,b与c的夹角为120°,且b*c=-4,a的模= 2020-06-12 …
已知平面上A,B,C三点的坐标分别为(-2,1),(-1,3)(3,4),且A,B,C,D这四点构 2020-06-14 …