早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC时(1)若CE⊥BD于E,①∠ECD=°;②求证:BD=2EC;(2)如图,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90&d
题目详情
如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC时
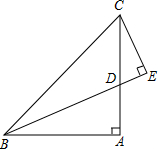
(1)若CE⊥BD于E,
①∠ECD=___°;
②求证:BD=2EC;
(2)如图,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点.当点P运动时,点Q是否一定在射线BD上?若在,请证明,若不在;请说明理由.

(1)若CE⊥BD于E,
①∠ECD=___°;
②求证:BD=2EC;
(2)如图,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点.当点P运动时,点Q是否一定在射线BD上?若在,请证明,若不在;请说明理由.
▼优质解答
答案和解析
(1)①∵∠BAC=90°,CE⊥BD,∠ADB=∠CDE,
∴∠ABD=∠ECD,
又∵∠BAC=90°,AB=AC,BD平分∠ABC,
∴∠ABD=22.5°,
∴∠ECD=22.5°;
故答案为:22.5.
②如图,延长CE交BA的延长线于点G,
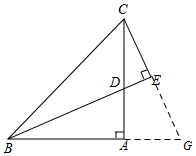
∵BD平分∠ABC,CE⊥BD,
∴CE=GE,
在△ABD与△ACG中,
,
∴△ABD≌△ACG(AAS),
∴BD=CG=2CE;
(2)点Q一定在射线BD上,
理由:如图,连接CQ,过点Q作QM⊥BP于M,作QN⊥BC于N,
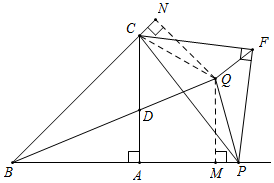
∵QF为∠PFC的角平分线,△CPF为等腰直角三角形,
∴QF为PC的垂直平分线,
∴PQ=QC,
∵Q为∠FPC与∠PFC的角平分线的交点,
∴CQ平分∠FCP,
∵△CPF为等腰直角三角形,
∴∠FCP=∠FPC=45°,
∴∠QCP=∠QPC=22.5°,
∴△PQC中,∠PQC=135°,
∵在四边形QNBM中,QM⊥BP,QN⊥BC,∠ABC=45°,
∴∠MQN=135°,
∴∠MQN=∠PQC,
∴∠NQC=∠MQP,
又∵QC=QP,QM⊥BP,QN⊥BC,
∴△QPM≌△QCN(AAS),
∴QM=QN,
又∵QM⊥BP,QN⊥BC,
∴点Q一定在射线BD上.
∴∠ABD=∠ECD,
又∵∠BAC=90°,AB=AC,BD平分∠ABC,
∴∠ABD=22.5°,
∴∠ECD=22.5°;
故答案为:22.5.
②如图,延长CE交BA的延长线于点G,

∵BD平分∠ABC,CE⊥BD,
∴CE=GE,
在△ABD与△ACG中,
|
∴△ABD≌△ACG(AAS),
∴BD=CG=2CE;
(2)点Q一定在射线BD上,
理由:如图,连接CQ,过点Q作QM⊥BP于M,作QN⊥BC于N,

∵QF为∠PFC的角平分线,△CPF为等腰直角三角形,
∴QF为PC的垂直平分线,
∴PQ=QC,
∵Q为∠FPC与∠PFC的角平分线的交点,
∴CQ平分∠FCP,
∵△CPF为等腰直角三角形,
∴∠FCP=∠FPC=45°,
∴∠QCP=∠QPC=22.5°,
∴△PQC中,∠PQC=135°,
∵在四边形QNBM中,QM⊥BP,QN⊥BC,∠ABC=45°,
∴∠MQN=135°,
∴∠MQN=∠PQC,
∴∠NQC=∠MQP,
又∵QC=QP,QM⊥BP,QN⊥BC,
∴△QPM≌△QCN(AAS),
∴QM=QN,
又∵QM⊥BP,QN⊥BC,
∴点Q一定在射线BD上.
看了 如图,在△ABC中,∠BAC...的网友还看了以下:
如图所示:直线MN⊥RS于点O,点B在射线OS上,OB=2,点C在射线ON上,OC=2,点E是射线 2020-05-13 …
如图所示:直线MN⊥RS于点O,点B在射线OS上,OB=2,点C在射线ON上,OC=2,点E是射线 2020-05-13 …
在边长为1的正方形ABCD中,点E是射线BC上一动点,AE与BD相交于点M,AE或其延长线与DC或 2020-05-17 …
已知∠MON=60°,射线OT是∠MON的平分线,点P是射线OT上的一个动点,射线PB交射线ON于 2020-05-21 …
△ABC中,∠C=90°,射线AD交射线BC于D,过D作DE垂直射线BA于点E,点F在射线CA上, 2020-06-06 …
已知∠MON=60°,射线OT是∠MON的平分线,点P是射线OT上的一个动点,射线PB交射线ON于 2020-06-23 …
如图,矩形ABCD中,AB=3,BC=4,点E是射线CB上的动点,点F是射线CD上一点,且AF⊥A 2020-07-17 …
如图,已知正方形ABCD的边长为4,E是射线CB上的一个动点,过点D作DF⊥DE,交BA的延长线与 2020-07-25 …
(2013•上海模拟)已知∠MON=60°,射线OT是∠MON的平分线,点P是射线OT上的一个动点, 2020-10-30 …
28.等边三角形ABC中,点E为直线AC上一点,在射线BE上取一点D,使角ADE=60度.(1)如图 2020-12-25 …