早教吧作业答案频道 -->数学-->
如图,矩形ABCD中,AB=3,BC=4,点E是射线CB上的动点,点F是射线CD上一点,且AF⊥AE,射线EF与对角线BD交于点G,与射线AD交于点M;(1)当点E在线段BC上时,求证:△AEF∽△ABD;(2)在(1)的
题目详情
如图,矩形ABCD中,AB=3,BC=4,点E是射线CB上的动点,点F是射线CD上一点,且AF⊥AE,射线EF与对角线BD交于点G,与射线AD交于点M;
(1)当点E在线段BC上时,求证:△AEF∽△ABD;
(2)在(1)的条件下,联结AG,设BE=x,tan∠MAG=y,求y关于x的函数解析式,并写出x的取值范围;
(3)当△AGM与△ADF相似时,求BE的长.

(1)当点E在线段BC上时,求证:△AEF∽△ABD;
(2)在(1)的条件下,联结AG,设BE=x,tan∠MAG=y,求y关于x的函数解析式,并写出x的取值范围;
(3)当△AGM与△ADF相似时,求BE的长.

▼优质解答
答案和解析
(1)证明:∵四边形ABCD是矩形,
∴∠BAD=∠ADC=∠ADF=90°,
∵AF⊥AE,
∴∠EAF=90°,
∴∠BAD=∠EAF,
∴∠BAE=∠DAF,∵∠ABE=∠ADF=90°,
∴△ABE∽△ADF,
∴
=
,
∴
=
,∵∠BAD=∠EAF,
∴△AEF∽△ABD.
(2) 如图连接AG.

∵△AEF∽△ABD,
∴∠ABG=∠AEG,
∴A、B、E、G四点共圆,
∴∠ABE+∠AGE=180°,
∵∠ABE=90°,
∴∠AGE=90°,
∴∠AGM=∠MDF,
∴∠AMG=∠FMD,
∴∠MAG=∠EFC,
∴y=tan∠MAG=tan∠EFC=
,
∵△ABE∽△ADF,
∴
=
,
∴DF=
x,
∴y=
,
即y=
(0≤x≤4).
(3) ①如图2中,当点E在线段CB上时,

∵△AGM∽ADF,
∴tan∠MAG=
=
,
∴
=
,
解得x=
.
②如图3中,当点E在CB的延长线上时,
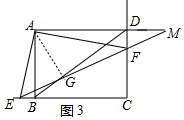
由△MAG∽△AFD∽△EFC,
∴
=
,
∴
=
,
解得x=1,
∴BE的长为
或1.
∴∠BAD=∠ADC=∠ADF=90°,
∵AF⊥AE,
∴∠EAF=90°,
∴∠BAD=∠EAF,
∴∠BAE=∠DAF,∵∠ABE=∠ADF=90°,
∴△ABE∽△ADF,
∴
| AB |
| AD |
| AE |
| AF |
∴
| AB |
| AE |
| AD |
| AF |
∴△AEF∽△ABD.
(2) 如图连接AG.

∵△AEF∽△ABD,
∴∠ABG=∠AEG,
∴A、B、E、G四点共圆,
∴∠ABE+∠AGE=180°,
∵∠ABE=90°,
∴∠AGE=90°,
∴∠AGM=∠MDF,
∴∠AMG=∠FMD,
∴∠MAG=∠EFC,
∴y=tan∠MAG=tan∠EFC=
| EC |
| CF |
∵△ABE∽△ADF,
∴
| AB |
| AD |
| BE |
| DF |
∴DF=
| 4 |
| 3 |
∴y=
| 4-x | ||
3+
|
即y=
| 12-3x |
| 9+4x |
(3) ①如图2中,当点E在线段CB上时,

∵△AGM∽ADF,
∴tan∠MAG=
| GM |
| AG |
| DF |
| AD |
∴
| 12-3x |
| 9+4x |
| ||
| 4 |
解得x=
| 3 |
| 2 |
②如图3中,当点E在CB的延长线上时,

由△MAG∽△AFD∽△EFC,
∴
| AD |
| EC |
| DF |
| FC |
∴
| 4 |
| x+4 |
| ||
3-
|
解得x=1,
∴BE的长为
| 3 |
| 2 |
看了 如图,矩形ABCD中,AB=...的网友还看了以下:
如图,在矩形ABCD中,∠CAB=30°,BC=43cm,将△ABC沿AC边翻折,使点B到点B′, 2020-05-13 …
如图,矩形ABCD中,AD=3厘米,AB=4厘米,N为BC上一点,BN=1厘米,动点M从B点出发, 2020-06-04 …
关于对称矩阵与反对称矩阵的一道题A是n阶对称矩阵B是n阶反对称矩阵下面哪个是反对称矩阵(A)AB− 2020-06-13 …
A,B均为n阶正交矩阵,且A^TB+B^TA+E≠0,则A.AB,A+B都是正交矩阵B.AB是正交 2020-06-18 …
在直角坐标系中,已知两点A(1,0),B(0,1),矩形OMPN的相邻两边OM,ON分别在x,y轴 2020-07-24 …
在长为12cm的线段AB上任取一点C,现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积小 2020-07-30 …
如图,折线A-B-C-D的每一条线段都平行于矩形的边,它把矩形分成面积相等的两部分.点E在矩形的边 2020-08-02 …
1.把一根2m的铁丝折弯成一个矩形框,并使矩形的宽和长之比成黄金比,求这个矩形的面积,)2.若点M 2020-08-02 …
如图,线段AB的长为202cm,点D在AB上,点AD上的△ACD是边长为10cm的等边三角形,过点 2020-08-03 …
下列有关图中逻辑斯蒂增长的说法,正确的是()A.这曲线是在理想条件下测得的,人工培养中不会出现这样的 2020-12-09 …