早教吧作业答案频道 -->数学-->
如图,在等边三角形△ABC中,AE=CD,AD、BE交于P点,BQ⊥AD于Q,(1)求证:BP=2PQ;(2)连PC,若BP⊥PC,求APPQ的值.
题目详情
如图,在等边三角形△ABC中,AE=CD,AD、BE交于P点,BQ⊥AD于Q,
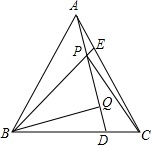
(1)求证:BP=2PQ;
(2)连PC,若BP⊥PC,求
的值.

(1)求证:BP=2PQ;
(2)连PC,若BP⊥PC,求
| AP |
| PQ |
▼优质解答
答案和解析
证明:(1)在等边△ABC中,AB=AC,∠BAE=∠ACD=60°,
在△BAE和△ACD中,
,
∴△BAE≌△ACD(SAS),
∴∠ABE=∠CAD,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°,
∵BQ⊥AD于Q,
∴∠BPQ=30°,
∴BP=2PQ;
(2)∵∠ABE=∠CAD,
∴∠ABC-∠ABE=∠BAC-∠CAD,
即∠PBC=∠BAQ,
在△BAQ和△CBP中,
,
∴△BAQ和△CBP(AAS),
∴AQ=BP=2PQ,
∴AP=PQ,
即
=1.
在△BAE和△ACD中,
|
∴△BAE≌△ACD(SAS),
∴∠ABE=∠CAD,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°,
∵BQ⊥AD于Q,
∴∠BPQ=30°,
∴BP=2PQ;
(2)∵∠ABE=∠CAD,
∴∠ABC-∠ABE=∠BAC-∠CAD,
即∠PBC=∠BAQ,
在△BAQ和△CBP中,
|
∴△BAQ和△CBP(AAS),
∴AQ=BP=2PQ,
∴AP=PQ,
即
| AP |
| PQ |
看了 如图,在等边三角形△ABC中...的网友还看了以下:
下列条件中,能作出唯一的三角形条件是()A已知三边做三角形B已知两边及一角做三角形C已知两角及一边做 2020-03-30 …
不能用来判断两个三角形全等的条件是()A.两角及夹边对应相等的两个三角形全等B.两边及夹角对应相等 2020-04-11 …
在一个三角形中,角越大,角所对的边更长.(对还是错)平形四边形有几条高?...在一个三角形中,角越 2020-05-13 …
1.在三角形ABC中,角C=90度,角A=30度,分别以AB、AC为边为三角形ABC的外边作等边三 2020-05-17 …
初二数学题追加2001.等边三角形的高是3CM,则它的边长为----2.直角三角形中,周长为2+根 2020-05-21 …
一个直角三角形中,一直边比另一直角边长4厘米,斜边的长比两直角边的和短8厘米,求这个直角三角形各边 2020-05-21 …
等边三角形的计算.下图是一个等边三角形,把等边三角形的各边中点连接起来,组成第二个等边三角形,再把 2020-06-03 …
1.在直角三角形中,30度所对的直角边长等于12厘米,则另一条直角边长是多少?2.等腰三角形的周长 2020-06-06 …
勾股定理速回,最好带点重要步骤.①在直角三角形中,已知一条直角边的长为15,斜边上的中线长为8.5 2020-06-27 …
1.在直角三角形中,如果2直角边的和为17,2直角之平方差为119,求斜边的长2.在三角形ABC中 2020-07-18 …