早教吧作业答案频道 -->数学-->
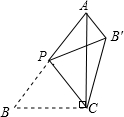
如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则下列判断:①当AP=BP时,AB′∥CP;②当AP=BP时,∠B
题目详情
如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则下列判断:
①当AP=BP时,AB′∥CP;
②当AP=BP时,∠B′PC=2∠B′AC
③当CP⊥AB时,AP=
;
④B′A长度的最小值是1.
其中正确的判断是___ (填入正确结论的序号)
①当AP=BP时,AB′∥CP;
②当AP=BP时,∠B′PC=2∠B′AC
③当CP⊥AB时,AP=
| 17 |
| 5 |
④B′A长度的最小值是1.
其中正确的判断是___ (填入正确结论的序号)

▼优质解答
答案和解析
①∵在△ABC中,∠ACB=90°,AP=BP,
∴AP=BP=CP,
∴∠B=∠BPC=
(180°-∠APB′),
由折叠的性质可得:CP=B′P,∠CPB′=∠BPC=
(180°-∠APB′),
∴AP=B′P,
∴∠AB′P=′B′AP=
(180°-∠APB′),
∴∠AB′P=∠CPB′,
∴AB′∥CP;故①正确;
②∵AP=BP,
∴PA=PB′=PC=PB,
∴点A,B′,C,B在以P为圆心,PA长为半径的圆上,
∵由折叠的性质可得:BC=B′C,
∴
=
,
∴∠B′PC=2∠B′AC;故②正确;
③当CP⊥AB时,∠APC=∠ACB,
∵∠PAC=∠CAB,
∴△ACP∽△ABC,
∴
=
,
∵在Rt△ABC中,由勾股定理可知:AC=
=
=4,
∴AP=
=
;故③错误;
④由轴对称的性质可知:BC=CB′=3,
∵CB′长度固定不变,
∴当AB′+CB′有最小值时,AB′的长度有最小值.
根据两点之间线段最短可知:A、B′、C三点在一条直线上时,AB′有最小值,
∴AB′=AC-B′C=4-3=1.故④正确.
故答案为:①②④.
∴AP=BP=CP,
∴∠B=∠BPC=
| 1 |
| 2 |
由折叠的性质可得:CP=B′P,∠CPB′=∠BPC=
| 1 |
| 2 |
∴AP=B′P,
∴∠AB′P=′B′AP=
| 1 |
| 2 |
∴∠AB′P=∠CPB′,
∴AB′∥CP;故①正确;
②∵AP=BP,
∴PA=PB′=PC=PB,
∴点A,B′,C,B在以P为圆心,PA长为半径的圆上,
∵由折叠的性质可得:BC=B′C,
∴
 |
| BC |
 |
| B′C |
∴∠B′PC=2∠B′AC;故②正确;
③当CP⊥AB时,∠APC=∠ACB,
∵∠PAC=∠CAB,
∴△ACP∽△ABC,
∴
| AP |
| AC |
| AC |
| AB |
∵在Rt△ABC中,由勾股定理可知:AC=
| AB2-BC2 |
| 52-32 |
∴AP=
| AC2 |
| AB |
| 16 |
| 5 |
④由轴对称的性质可知:BC=CB′=3,
∵CB′长度固定不变,
∴当AB′+CB′有最小值时,AB′的长度有最小值.
根据两点之间线段最短可知:A、B′、C三点在一条直线上时,AB′有最小值,
∴AB′=AC-B′C=4-3=1.故④正确.
故答案为:①②④.
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
圆锥曲线若直线y=x-b与抛物线y2=2px(p>0)相交于不同两点A(x1,y1),B(x2,y 2020-06-12 …
逻辑充分假言命题,为何如果P则Q,等价与非p或者q,根据肯前肯后或者否前否后的原则,我推不出逻辑充 2020-07-01 …
若p,则q,的形式命题中,此命题中的q是否是p的必要条件?若(x-a)(x-b)=0,则x=a若p 2020-08-01 …
关于命题的否定和否命题原名题若P则Q否命题为若非P则非Q命题的否定为若关于命题的否定和否命题原名题 2020-08-01 …
否命题的问题1若P则Q的否命题是:若非P则非Q;若P则Q,它的命题的否是:P且非Q;那P且非Q,它 2020-08-01 …
在下列横线上填写“互逆”“互否”“互为逆否”或“互为否定形式”:(1)命题“若q则p”与“若q则p 2020-08-02 …
与命题“若p则¬q”等价的命题为()A.若p则qB.若¬p则qC.若q则¬pD.若¬q则p 2020-08-02 …
设语句p:x=-9,非q:x2+8x-9=0,则下列命题为真命题的是[]A.p且qB.p或qC.若p 2020-12-07 …
命题“若p则q”的否定是()A.若p则¬qB.若¬p则¬qC.若¬q则¬pD.若q则p 2020-12-09 …
已知点P(-4,3)先向左平移2个单位,再向下平移2个单位得点P‘,则点P’的坐标为()若点P(a, 2020-12-24 …