早教吧作业答案频道 -->数学-->
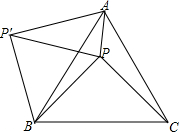
如图,P是正△ABC内一点,∠APC=130°,将△BPC绕点B逆时针方向旋转60°得到△BP′A,连接PP′,当∠BPC为多少度时,△APP′是等腰三角形?
题目详情
如图,P是正△ABC内一点,∠APC=130°,将△BPC绕点B逆时针方向旋转60°得到△BP′A,连接PP′,当∠BPC为多少度时,△APP′是等腰三角形?

▼优质解答
答案和解析
∵PB=P′B,∠PBP′=60°,
∴△P′PB是等边三角形,
∴∠P′PB=∠PP′B=60°,
设∠BPC=x时,由△APP′是等腰三角形,则∠AP′B=x,
∴∠AP′P=x-60°,
①当P′A=P′P时,则∠P′PA=∠PAP′=
,
∵∠APP′+∠P′PB+∠BPC+∠APC=360°,
∴
+60°+x+130°=360°,
解得x=100°;
②当P′A=PA时,则∠P′PA=∠PP′A=x-60°
∵∠APP′+∠P′PB+∠BPC+∠APC=360°,
∴x-60°+60°+x+130°=360°,
解得x=115°;
③当P′P=PA时,则∠P′PA=180°-2(x-60°)=300°-2x
∵∠APP′+∠P′PB+∠BPC+∠APC=360°,
∴300°-2x+60°+x+130°=360°,
解得x=130°;
所以,当∠BPC为100°或115°或130°,△APP′是等腰三角形.
∴△P′PB是等边三角形,
∴∠P′PB=∠PP′B=60°,
设∠BPC=x时,由△APP′是等腰三角形,则∠AP′B=x,
∴∠AP′P=x-60°,
①当P′A=P′P时,则∠P′PA=∠PAP′=
| 180°-(x-60°) |
| 2 |
∵∠APP′+∠P′PB+∠BPC+∠APC=360°,
∴
| 180°-(x-60°) |
| 2 |
解得x=100°;
②当P′A=PA时,则∠P′PA=∠PP′A=x-60°
∵∠APP′+∠P′PB+∠BPC+∠APC=360°,
∴x-60°+60°+x+130°=360°,
解得x=115°;
③当P′P=PA时,则∠P′PA=180°-2(x-60°)=300°-2x
∵∠APP′+∠P′PB+∠BPC+∠APC=360°,
∴300°-2x+60°+x+130°=360°,
解得x=130°;
所以,当∠BPC为100°或115°或130°,△APP′是等腰三角形.
看了 如图,P是正△ABC内一点,...的网友还看了以下:
在三角形ABC中,AC=BC>AB,点P为三角形ABC所在平面内一点,且点P与三角形ABC的任意两 2020-05-15 …
求:直线的位置关系--夹角.点P是直线L上的点,将直线L绕P沿逆时针方向旋转a(0 2020-06-04 …
老师您好,我能请教您一个几何问题吗?希望给予解答.谢谢!在等腰直角三角形ABC中,角C为直角,点P 2020-06-14 …
已知:如图,点M在锐角角AOB的内部,在OB边上求作一点P,使得点P到点M的距离与点P到OA边的已 2020-07-22 …
如图(1),凸四边形ABCD,如果点P满足∠APD=∠APB=α,且∠BPC=∠CPD=β,则称点 2020-07-25 …
(2006•安徽)如图(1),凸四边形ABCD,如果点P满足∠APD=∠APB=α.且∠BPC=∠ 2020-07-25 …
已知三角形ABC,P为三角形所在平面上的动点点,且点P满足PA·PC+PA·PB+PB·PC=0则 2020-07-30 …
定直线与面成45度角,点P是面内一动点,且点P到定直线的距离为2,求动点P轨迹的离心率.我求的答案 2020-07-31 …
已知a是第二象限角,点p(x,√5)在其中边上,若cosa=√2/4x.求x的值.求sina的值. 2020-08-03 …
以x轴为正方向,y轴正方向为边,以原点为顶点的角成为第一象限角,已知直线l评分第一现象角,点P(1, 2021-01-17 …