早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系xOy中,点O为坐标原点,矩形AOCD的边OC、OA分别在x轴、y轴上,点D的坐标为(6,4),点P是线段AD边上的任意一点(不含端点A、D),连结PC,过点P作PE⊥PC交AO于E点.
题目详情
如图,在平面直角坐标系xOy中,点O为坐标原点,矩形AOCD的边OC、OA分别在x轴、y轴上,点D的坐标为(6,4),点P是线段AD边上的任意一点(不含端点A、D),连结PC,过点P作PE⊥PC交AO于E点.
(1)当点P坐标为(4,4)时,求点E的坐标;
(2)当点P坐标为(5,4)时,在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)当点P在AD上运动时,对应的点E也随之在AO上运动,求OE的取值范围.
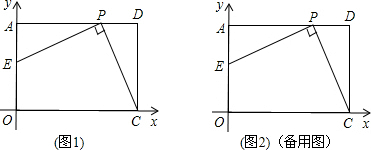
(1)当点P坐标为(4,4)时,求点E的坐标;
(2)当点P坐标为(5,4)时,在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)当点P在AD上运动时,对应的点E也随之在AO上运动,求OE的取值范围.

▼优质解答
答案和解析
(1)∵∠EAD=∠EPC=∠PDC,
∴∠APE=∠DCP,
,
∴△APE≌△DCP,
∴AE=PD=2,
∴点E(0,2);
(2)存在这样的点Q,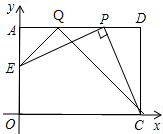
假设存在这样的点Q,
∵∠EAP=∠EPC=∠PDC,
∴△APE∽△DCP,
∴
=
,
∵AP=5,CD=4,DP=1,
∴AE=
,
∵∠EAQ=∠EQC=∠QDC,
∴△QAE∽△CDQ,
∴
=
,
设AQ=x,
=
,
解得x=1或x=5,当x=5时点Q与点P重合,故舍去,
所以存在这样的点Q,其坐标为(1,4);
(3)设AP=x,AE=y,
∵△APE∽△DCP,
∴
=
,
∴
=
,
∴y=-
x2+
x,
当x=3时(在0<x<6范围内),y最大值=
,
又∵E在AB上运动,且AO=4,
∴OE的最小值为4-
=
,
∴OE的取值范围是
≤BE<4.
∴∠APE=∠DCP,
|
∴△APE≌△DCP,
∴AE=PD=2,
∴点E(0,2);
(2)存在这样的点Q,

假设存在这样的点Q,
∵∠EAP=∠EPC=∠PDC,
∴△APE∽△DCP,
∴
| AP |
| DC |
| AE |
| DP |
∵AP=5,CD=4,DP=1,
∴AE=
| 5 |
| 4 |
∵∠EAQ=∠EQC=∠QDC,
∴△QAE∽△CDQ,
∴
| AQ |
| CD |
| AE |
| DQ |
设AQ=x,
| x |
| 4 |
| ||
| 6-x |
解得x=1或x=5,当x=5时点Q与点P重合,故舍去,
所以存在这样的点Q,其坐标为(1,4);
(3)设AP=x,AE=y,
∵△APE∽△DCP,
∴
| AP |
| DC |
| AE |
| DP |
∴
| x |
| 4 |
| y |
| 6-x |
∴y=-
| 1 |
| 4 |
| 3 |
| 2 |
当x=3时(在0<x<6范围内),y最大值=
| 9 |
| 4 |
又∵E在AB上运动,且AO=4,
∴OE的最小值为4-
| 9 |
| 4 |
| 7 |
| 4 |
∴OE的取值范围是
| 7 |
| 4 |
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
(2009•长宁区二模)手t,曲线C:y=2x(0≤x≤2)两端分别为M、2,且2图⊥x轴于点图. 2020-05-15 …
(2012•金衢十一校一模)如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y 2020-06-10 …
等边三角形ABC的边长为6,将其放置在如图所示的平面直角坐标系中,其中BC边在x轴上,BC边的高O 2020-06-23 …
如图是一条线段.①以线段AB为直径画一个圆.②再以这条线段为边画一个正方形.③画出这个组合图形的对 2020-07-13 …
如图,在平面直角坐标系xOy中,点O为坐标原点,矩形AOCD的边OC、OA分别在x轴、y轴上,点D 2020-07-24 …
如图,在平面直角坐标系xOy中,角α(0≤α≤π)的始边为x轴的非负半轴,终边与单位圆的交点为A, 2020-07-30 …
(本题满分10分)如图,直角坐标系中,点的坐标为,以线段为边在第四象限内作等边,点为正半轴上一动点 2020-08-01 …
线段C:y=x+2(0≤x≤2)两端分别为M、N,且NA⊥x轴于点A.把线段OA分成n等份,以每一 2020-08-02 …
下列说法正确的是()A.轴对称涉及两个图形,轴对称图形涉及一个图形B.如果两条线段互相垂直平分,那么 2020-11-08 …
数学题...下面4句话中,不正确的是()A平行四边形容易变形.B平行四边形一定是轴对称图形.C直角梯 2021-02-02 …