早教吧作业答案频道 -->数学-->
以直线AB上一点O为端点作射线OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE=°;(2)如图2
题目详情
以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE=___°;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=
∠AOE,求∠BOD的度数?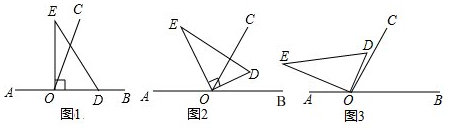
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE=___°;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=
| 1 |
| 5 |

▼优质解答
答案和解析
(1)∵∠BOE=∠COE+∠COB=90°,
又∵∠COB=60°,
∴∠COE=30°,
故答案为:30;
(2)∵OE平分∠AOC,
∴∠COE=∠AOE=
∠COA,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,
∴∠COD=∠DOB,
∴OD所在射线是∠BOC的平分线;
(3)设∠COD=x°,则∠AOE=5x°,
∵∠DOE=90°,∠BOC=60°,
∴6x=30,
∴x=5,
即∠COD=5°,
∵∠BOC=60°,
∴∠BOD=∠BOC+∠COD=65°.
又∵∠COB=60°,
∴∠COE=30°,
故答案为:30;
(2)∵OE平分∠AOC,
∴∠COE=∠AOE=
| 1 |
| 2 |
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,
∴∠COD=∠DOB,
∴OD所在射线是∠BOC的平分线;
(3)设∠COD=x°,则∠AOE=5x°,
∵∠DOE=90°,∠BOC=60°,
∴6x=30,
∴x=5,
即∠COD=5°,
∵∠BOC=60°,
∴∠BOD=∠BOC+∠COD=65°.
看了 以直线AB上一点O为端点作射...的网友还看了以下:
如图,△ABD是O的内接三角形,E是弦BD的中点,点C是O外一点且∠DBC=∠A,连接OE延长与圆 2020-07-11 …
(2014•白银)如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影 2020-07-20 …
如图已知圆形O的半径为6,P是半径OA上的一个动点(不包括端点),过点P作OA垂线交圆形O于B,C 2020-07-31 …
如图,矩形OABC的顶点坐标分别为O(0,0)、A(6,0)、B(6,4)、C(0,4),画出以点 2020-08-02 …
在直角坐标系中,ΔABO的顶点A坐标为A(6,0),O为原点,AB=8,∠BAO=60度,ΔABO绕 2020-11-04 …
在平面直角坐标中,四边形OABC是等腰梯形,CB平行于OA,OC=AB=4,BC=6,角COA=45 2020-11-13 …
如图,梯形ABCD中,AD∥BC,CD⊥BC,已知AB=5,BC=6,cosB=35.点O为BC边上 2020-12-08 …
圆o过点B,C,圆心o在等腰直角三角形内部(急,1.(2010安徽省中中考)如图,⊙O过点B、C.圆 2020-12-12 …
如图矩形ABCD中AB=6BC=2√3点O是AB的中点点P在AB的延长线上且BP=3一动点E从O点出 2021-01-02 …
如图,⊙O的半径为6,点C在⊙O上,将圆折叠,使点C与圆心O重合,折痕为AB且点A、B在⊙O上,E、 2021-01-22 …