早教吧作业答案频道 -->数学-->
如图,动点M在以O为圆心,AB为直径的半圆弧上运动(点M不与点A、B及AB的中点F重合),连接OM.过点M作ME⊥AB于点E,以BE为边在半圆同侧作正方形BCDE,过点M作⊙O的切线交射线DC于点N,连
题目详情
如图,动点M在以O为圆心,AB为直径的半圆弧上运动(点M不与点A、B 及
的中点F 重合),连接OM.过点M 作ME⊥AB于点E,以BE为边在半圆同侧作正方形BCDE,过点M作⊙O的切线交射线DC于点N,连接BM、BN.
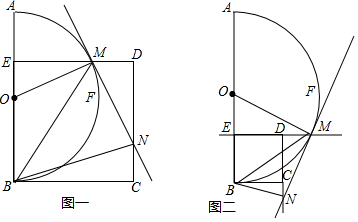
(1)探究:如图一,当动点M在
上运动时;
①判断△OEM∽△MDN是否成立?请说明理由;
②设
=k,k是否为定值?若是,求出该定值,若不是,请说明理由;
③设∠MBN=α,α是否为定值?若是,求出该定值,若不是,请说明理由;
(2)拓展:如图二,当动点M 在
上运动时;
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)
 |
| AB |

(1)探究:如图一,当动点M在
 |
| AF |
①判断△OEM∽△MDN是否成立?请说明理由;
②设
| ME+NC |
| MN |
③设∠MBN=α,α是否为定值?若是,求出该定值,若不是,请说明理由;
(2)拓展:如图二,当动点M 在
 |
| FB |
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)
▼优质解答
答案和解析
(1)①△OEM∽△MDN成立,理由如下:
∵四边形BCDE是正方形,
∴BE=BC,∠EBC=∠CDE=∠BCD=∠BED=90°,
∴∠EOM+∠EMO=90°,
∵MN是⊙O的切线,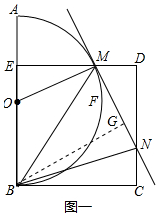
∴MN⊥OM,
∴∠OMN=90°,
∴∠DMN+∠EMO=90°,
∴∠EOM=∠DMN,
∴△OEM∽△MDN;
②k值为定值1;理由如下:
作BG⊥MN于G,如图一所示:
则BG∥OM,∠BGN=∠BGM=90°,
∴∠OMB=∠GBM,
∵OB=OM,
∴∠OBM=∠OMB,
∴∠OBM=∠GBM,
在△BME和△BMG中,
,
∴△BME≌△BMG(AAS),
∴EM=GM,BE=BG,
∴BG=BC,
在Rt△BGN和Rt△BCN中,
,
∴Rt△BGN≌Rt△BCN(HL),
∴GN=CN,
∴EM+NC=GM+NC=MN,
∴k=
=
=1;
③设∠MBN=α,α为定值45°;理由如下:
∵△BME≌△BMG,Rt△BGN≌Rt△BCN,
∴∠EBM=∠GBM,∠GBN=∠CBN,
∴∠MBN=
∠EBC=45°,
即α=45°;
(2)(1)中的三个结论保持不变;理由同(1),作BG⊥MN于G,如图二所示.
∵四边形BCDE是正方形,
∴BE=BC,∠EBC=∠CDE=∠BCD=∠BED=90°,
∴∠EOM+∠EMO=90°,
∵MN是⊙O的切线,

∴MN⊥OM,
∴∠OMN=90°,
∴∠DMN+∠EMO=90°,
∴∠EOM=∠DMN,
∴△OEM∽△MDN;
②k值为定值1;理由如下:
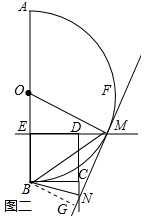
作BG⊥MN于G,如图一所示:
则BG∥OM,∠BGN=∠BGM=90°,
∴∠OMB=∠GBM,
∵OB=OM,
∴∠OBM=∠OMB,
∴∠OBM=∠GBM,
在△BME和△BMG中,
|
∴△BME≌△BMG(AAS),
∴EM=GM,BE=BG,
∴BG=BC,
在Rt△BGN和Rt△BCN中,
|

∴Rt△BGN≌Rt△BCN(HL),
∴GN=CN,
∴EM+NC=GM+NC=MN,
∴k=
| ME+NC |
| MN |
| MN |
| MN |
③设∠MBN=α,α为定值45°;理由如下:
∵△BME≌△BMG,Rt△BGN≌Rt△BCN,
∴∠EBM=∠GBM,∠GBN=∠CBN,
∴∠MBN=
| 1 |
| 2 |
即α=45°;
(2)(1)中的三个结论保持不变;理由同(1),作BG⊥MN于G,如图二所示.
看了 如图,动点M在以O为圆心,A...的网友还看了以下:
爱与感动作文 2020-07-04 …
如图所示,虚线MN将平面分成I和II两个区域,两个区域都存在与纸面垂直的匀强磁场.一带电粒子仅在磁 2020-07-20 …
人生的爱好者我们晓得如果我们把积极的和消极的人生观念适当地混合起来,我们能够得到一种和谐的中庸哲学 2020-07-29 …
想法与行动作文 2020-11-06 …
沉稳与灵动作文 2020-12-20 …
沉稳与灵动作文 2020-12-20 …
沉稳与灵动作文 2020-12-20 …
沉稳与灵动作文 2020-12-20 …
阅读下面文章,完成后面问题。人生的爱好者我们晓得如果我们把积极的和消极的人生观念适当地混合起来,我们 2021-01-16 …
如图所示,虚线MN将平面分成I和Ⅱ两个区域,两个区域都存在与纸面垂直的匀强磁场.一带电粒子仅在磁场力 2021-01-17 …