早教吧作业答案频道 -->数学-->
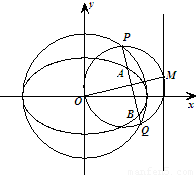
如图,已知椭圆方程为,O为原点,点M是椭圆右准线上的动点,以OM为直径的圆与以椭圆长轴为直径的圆交于P、Q两点,直线PQ与椭圆相交于A、B两点,则|AB|的取值范围是()A.B
题目详情
如图,已知椭圆方程为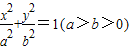 ,O为原点,点M是椭圆右准线上的动点,以OM为直径的圆与以椭圆长轴为直径的圆交于P、Q两点,直线PQ与椭圆相交于A、B两点,则|AB|的取值范围是( )
,O为原点,点M是椭圆右准线上的动点,以OM为直径的圆与以椭圆长轴为直径的圆交于P、Q两点,直线PQ与椭圆相交于A、B两点,则|AB|的取值范围是( )
A.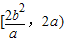
B.
C.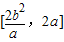
D.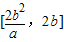
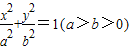 ,O为原点,点M是椭圆右准线上的动点,以OM为直径的圆与以椭圆长轴为直径的圆交于P、Q两点,直线PQ与椭圆相交于A、B两点,则|AB|的取值范围是( )
,O为原点,点M是椭圆右准线上的动点,以OM为直径的圆与以椭圆长轴为直径的圆交于P、Q两点,直线PQ与椭圆相交于A、B两点,则|AB|的取值范围是( )
A.
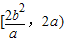
B.

C.
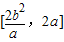
D.
▼优质解答
答案和解析
【答案】 分析: 确定以OM为直径的圆与以椭圆长轴为直径的圆的方程,利用图形的对称性,即可求得结论.
设M(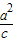 ,m),则以OM为直径的圆的方程为
,m),则以OM为直径的圆的方程为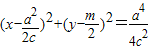 +
+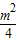 ①
①
以椭圆长轴为直径的圆的方程为x 2 +y 2 =a 2 ②
根据图形可知,当M在x轴上时,|AB|最小,此时方程①为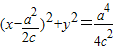 ③
③
②-③可得:x=c,代入椭圆方程,可得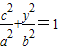 ,∴y=±
,∴y=±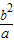 ,∴|AB|=
,∴|AB|=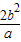
当M在无穷远时,|AB|最大,以OM为直径的圆与以椭圆长轴为直径的圆交于长轴的端点,∴|AB|→2a
∴|AB|的取值范围是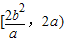
故选A.
点评: 本题考查圆的方程,考查圆与椭圆的综合,解题的关键是确定圆的方程,属于中档题.
设M(
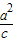 ,m),则以OM为直径的圆的方程为
,m),则以OM为直径的圆的方程为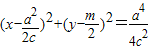 +
+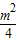 ①
①以椭圆长轴为直径的圆的方程为x 2 +y 2 =a 2 ②
根据图形可知,当M在x轴上时,|AB|最小,此时方程①为
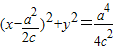 ③
③②-③可得:x=c,代入椭圆方程,可得
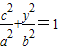 ,∴y=±
,∴y=±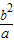 ,∴|AB|=
,∴|AB|=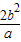
当M在无穷远时,|AB|最大,以OM为直径的圆与以椭圆长轴为直径的圆交于长轴的端点,∴|AB|→2a
∴|AB|的取值范围是
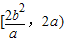
故选A.
点评: 本题考查圆的方程,考查圆与椭圆的综合,解题的关键是确定圆的方程,属于中档题.
看了 如图,已知椭圆方程为,O为原...的网友还看了以下:
已知点P是圆x^2+y^2=16上的一个动点,点A是x轴上的定点,坐标为(12,0).当点P在圆上 2020-05-13 …
已知椭圆C的左、右焦点坐标分别是(-根号2,0),(根号2,0),离心率是根号6/3,直线y=t椭 2020-05-16 …
已知动圆P过定点A(-3,0),并且与定圆B:(x-3)2+y2=64内切,则动圆的圆心P的轨迹是 2020-05-17 …
高一直线与圆的位置关系的题!1.已知点P(2.0)及圆C:x^2+y^2-6x+4y+4=0.设过 2020-06-07 …
已知椭圆C的中心在原点,焦点在轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1F2B2是一个 2020-06-21 …
(本小题满分12分)已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外 2020-06-30 …
已知点P为椭圆上任意一点,点P到直线L1:x=2的距离为d1,到点F1(1,0)的距离为d2,且d 2020-07-09 …
已知点P在以坐标轴为对称轴的椭圆上,点P到两个焦点的距离分别为和,过P作焦点所在轴已知点P在以坐标 2020-07-13 …
(2013•安阳模拟)已知圆C1:(x+62)2+y2=258,圆C2:(x-62)2+y2=18 2020-07-19 …
已只圆心p的半径为2,圆心P在抛物线y=1/2x的平方-1上运动,当圆心p与x轴相切,圆心p的坐标 2020-07-21 …