早教吧作业答案频道 -->数学-->
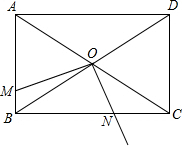
如图,O为矩形ABCD对角线的交点,M为AB边上任一点,射线ON⊥OM于点O,且与BC边交于点N,若AB=4,AD=6,则四边形OMBN面积的最大值为.
题目详情
如图,O为矩形ABCD对角线的交点,M为AB边上任一点,射线ON⊥OM于点O,且与BC边交于点N,若AB=4,AD=6,则四边形OMBN面积的最大值为___.

▼优质解答
答案和解析
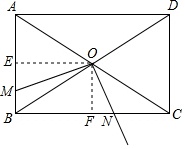 (方法一)过点O作OE⊥AB于点E,作OF⊥BC于点F,如图所示.
(方法一)过点O作OE⊥AB于点E,作OF⊥BC于点F,如图所示.
∵四边形ABCD为矩形,AB=4,AD=6,
∴OE=3,OF=2,OE⊥OF,
∴∠EOM+∠FOM=90°,
∵∠FON+∠FOM=90°,
∴∠EOM=∠FON.
∵∠OEM=∠OFN=90°,
∴△FON∽△EOM,
∴OM:ON=OE:OF=3:2,
∴
=
.
设ME=x(0≤x≤2),则FN=
x,
∴S四边形OMBN=S矩形EBFO-S△EOM+S△FON=2×3-
×3x+
×2×
x=-
x+6,
∴当x=0时,S四边形OMBN取最大值,最大值为6.
故答案为:6.
(方法二)过点O作OE⊥AB于点E,作OF⊥BC于点F,当点M和点E重合、点N和点F重合时,四边形OMBN面积取最大值,如图所示.
∵S矩形EBFO=2×3=6,
∴四边形OMBN面积的最大值为6.
故答案为:6
 (方法一)过点O作OE⊥AB于点E,作OF⊥BC于点F,如图所示.
(方法一)过点O作OE⊥AB于点E,作OF⊥BC于点F,如图所示.∵四边形ABCD为矩形,AB=4,AD=6,
∴OE=3,OF=2,OE⊥OF,
∴∠EOM+∠FOM=90°,
∵∠FON+∠FOM=90°,
∴∠EOM=∠FON.
∵∠OEM=∠OFN=90°,
∴△FON∽△EOM,
∴OM:ON=OE:OF=3:2,
∴
| S△OEM |
| S△OFN |
| 9 |
| 4 |
设ME=x(0≤x≤2),则FN=
| 2 |
| 3 |
∴S四边形OMBN=S矩形EBFO-S△EOM+S△FON=2×3-
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
∴当x=0时,S四边形OMBN取最大值,最大值为6.
故答案为:6.
(方法二)过点O作OE⊥AB于点E,作OF⊥BC于点F,当点M和点E重合、点N和点F重合时,四边形OMBN面积取最大值,如图所示.
∵S矩形EBFO=2×3=6,
∴四边形OMBN面积的最大值为6.
故答案为:6
看了 如图,O为矩形ABCD对角线...的网友还看了以下:
如图,三角形ABC为等边三角形,D是边BC上[除B,C外]的任意一点,角ADE=60度,且DE交角 2020-04-27 …
七下数学图形的全等工人师傅常用角尺平分一个任意角,如图,角AOB是一个任意角,在边OA,OB上分别 2020-05-17 …
以下试题最好用初中知识解答,实在不行再用四点共圆.图略.如图在等边三角形ABC的边BC上任取一点D 2020-06-06 …
在三角形的每条边上各取三个分点(如图),以这9个分点为顶点可画出若干个三角形,若从中任意抽取一个三 2020-07-13 …
三角形BPE与PFE相似吗?为什么?三角形ABC为等腰直角三角形,其中角B=角C=30°,三角形P 2020-08-01 …
如图,已知AB是半圆O的直径,AB=8,M、N、P是将半圆圆周四等分的三个分点(1)从A、B、M、 2020-08-01 …
书上的..初二下册第151页的第18题如图,在三角形ABC中,1.P是三角形ABC内任意一点,角B 2020-08-03 …
我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I 2020-11-02 …
从下图15个点中任取3个点,可以画出多少个三角形图画不出,就是阶梯三角形(每三点之间距离相等第一层1 2020-11-24 …
一个图论题平面中有100个点(任3点不在一直线上),证明,可以用2500条边把这100个顶点连成一个 2020-12-13 …