为什么登山者选择曲径登顶，滑雪者选择曲线奔向终点，河流选择蜿蜒流向大海？原来经过试验和论证，两点间最快的路线并不是直线，而是一段旋轮线，也被称为“最速曲线”。两点之间

题目详情

为什么登山者选择曲径登顶，滑雪者选择曲线奔向终点，河流选择蜿蜒流向大海？原来经过试验和论证，两点间最快的路线并不是直线，而是一段旋轮线，也被称为“最速曲线”。两点之间最短距离是直线，但选择曲线也许是解决问题的最快路径，这是因为（　　）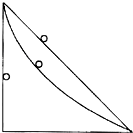
作业帮

A. 创新有助于改变思维方式借势而行

B. 成功的路径取决于创新的思维方式

C. 质疑权威否定一切有助于开拓创新

D. 创新意识是推动实践发展的根本动力

▼优质解答

答案和解析

A符合题意，材料中强调并没有走直线，而是旋轮线，这是一种创新的思维方式，说明创新有助于改变思维方式借势而行；
B说法错误，创新的思维方式对成功的路径不能起决定作用；
C说法错误，创新不代表肯定一切，也不代表否定一切；
D说法错误，社会基本矛盾是推动社会发展的根本动力．
故本题选A．

看了为什么登山者选择曲径登顶，滑...的网友还看了以下：