早教吧作业答案频道 -->数学-->
已知∠MAN=135°,正方形ABCD绕点A旋转.(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM、AN分别与正方形ABCD的边CB、CD的延长线交于点M、N,连接MN.①如图1,若BM=DN,则线段MN与BM+DN
题目详情
已知∠MAN=135°,正方形ABCD绕点A旋转.
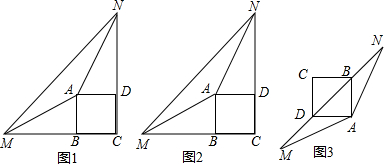
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM、AN分别与正方形ABCD的边CB、CD的延长线交于点M、N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是___
②如图2,若BM≠DN,请判断①中的数量关系关系是否仍成立?并说明理由.
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM、AN分别与直线BD交于点M、N,探究:以线段BM、DN的长度为三边长的三角形是何种三角形?并说明理由.

(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM、AN分别与正方形ABCD的边CB、CD的延长线交于点M、N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是___
②如图2,若BM≠DN,请判断①中的数量关系关系是否仍成立?并说明理由.
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM、AN分别与直线BD交于点M、N,探究:以线段BM、DN的长度为三边长的三角形是何种三角形?并说明理由.
▼优质解答
答案和解析
(1)①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是MN=BM+DN.理由如下:
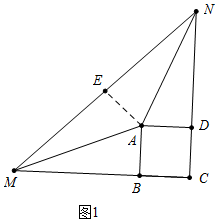
在△ADN与△ABM中,
,
∴△ADN≌△ABM(SAS),
∴AN=AM,∠NAD=∠MAB,
∵∠MAN=135°,∠BAD=90°,
∴∠NAD=∠MAB=
(360°-135°-90°)=67.5°,
作AE⊥MN于E,则MN=2NE,∠NAE=
∠MAN=67.5°.
在△ADN与△AEN中,
,
∴△ADN≌△AEN(AAS),
∴DN=EN,
∵BM=DN,MN=2EN,
∴MN=BM+DN.
故答案为MN=BM+DN;
②如图2,若BM≠DN,①中的数量关系仍成立.理由如下:
将△ABM绕点A逆时针旋转90°得到△ADE,易知N、D、E三点共线.
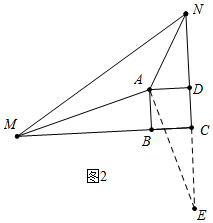
∵AM=AP,∠MAE=90°
∴∠EAN=360°-∠MAN-∠MAE=360°-135°-90°=135°,
∴∠MAN=∠NAE,
在△ANM与△ANP中,
,
∴△ANM≌△ANE(SAS),
∴MN=EN,
∵EN=DE+DN=BM+DN,
∴MN=BM+DN;
(2)结论:以线段BM、DN的长度为三边长的三角形是直角三角形.
理由:将△ABM绕点A逆时针旋转90°得到△ADE,连接NE,
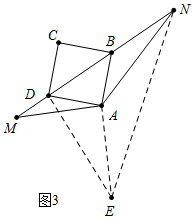
∵∠MAE=90°,∠MAN=135°,
∴∠NAE=360°-∠MAN-∠MAE=135°
∴∠EAN=∠MAN,
∵AM=AE,AN=AN,
∴△AMN≌△AEN,
∴MN=EN,
∵∠ADE=∠ABM=∠BDA=45°,
∴∠BDE=∠BDA+∠ADE=90°
∴DN2+DE2=NE2,∵BM=DE,MN=EN,
∴DN2+BM2=MN2
∴以线段BM、MN、DN的长度为三边长的三角形是直角三角形.

在△ADN与△ABM中,
|
∴△ADN≌△ABM(SAS),
∴AN=AM,∠NAD=∠MAB,
∵∠MAN=135°,∠BAD=90°,
∴∠NAD=∠MAB=
| 1 |
| 2 |
作AE⊥MN于E,则MN=2NE,∠NAE=
| 1 |
| 2 |
在△ADN与△AEN中,
|
∴△ADN≌△AEN(AAS),
∴DN=EN,
∵BM=DN,MN=2EN,
∴MN=BM+DN.
故答案为MN=BM+DN;
②如图2,若BM≠DN,①中的数量关系仍成立.理由如下:
将△ABM绕点A逆时针旋转90°得到△ADE,易知N、D、E三点共线.

∵AM=AP,∠MAE=90°
∴∠EAN=360°-∠MAN-∠MAE=360°-135°-90°=135°,
∴∠MAN=∠NAE,
在△ANM与△ANP中,
|
∴△ANM≌△ANE(SAS),
∴MN=EN,
∵EN=DE+DN=BM+DN,
∴MN=BM+DN;
(2)结论:以线段BM、DN的长度为三边长的三角形是直角三角形.
理由:将△ABM绕点A逆时针旋转90°得到△ADE,连接NE,

∵∠MAE=90°,∠MAN=135°,
∴∠NAE=360°-∠MAN-∠MAE=135°
∴∠EAN=∠MAN,
∵AM=AE,AN=AN,
∴△AMN≌△AEN,
∴MN=EN,
∵∠ADE=∠ABM=∠BDA=45°,
∴∠BDE=∠BDA+∠ADE=90°
∴DN2+DE2=NE2,∵BM=DE,MN=EN,
∴DN2+BM2=MN2
∴以线段BM、MN、DN的长度为三边长的三角形是直角三角形.
看了 已知∠MAN=135°,正方...的网友还看了以下:
(1)将图形①绕点A(3,5)逆时针旋转90°,画出旋转后的图形.旋转后,点B的位置用数对表示是( 2020-04-06 …
空间坐标系的转化问题中需要用到旋转矩阵R和平移矩阵T,其中R为3x3的正交旋转变换矩阵,T为3xl 2020-06-14 …
如图①,在Rt△ABC中,∠C=90°.将△ABC绕点C逆时针旋转得到△A′B′C,旋转角为BP= 2020-06-15 …
把正确答案的序号填在横线里.A.平移B.旋转C.对称D.放大E.缩小(1)钟面上分针和时针的转动. 2020-06-28 …
(2013·高考浙江卷)下列词语中加点的字,注音全都正确的一项是()A.旋涡(xuán)按捺(nà 2020-06-29 …
已知在△ABC中,∠C=90°,AC=3,BC=4.在平面内将△ABC绕B点旋转,点A落到A′,点 2020-07-04 …
拉开抽屉的运动是,螺旋桨的运动是.A.平移B.旋转C.既是平移又是旋转. 2020-07-04 …
下列说法中错误的是()A.旋转中心到对应点的距离相等B.对称中心是对称点所连线段的中点C.旋转后的 2020-08-01 …
下列说法正确的是()A.旋转后重合的两个图形成中心对称B.全等的两个图形一定成中心对称C.成中心对 2020-08-03 …
下列描述正确的是()A.旋转后得到的图形与原图形形状与大小都发生变化B.旋转后得到的图形与原图形形 2020-08-03 …