早教吧作业答案频道 -->数学-->
如图,已知二次函数y1=-x2+134x+c的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为y2=kx+b.(1)求二次函数y1的解析式及点B的坐标;(2)由图象写出满足y1<y2的自变量x的
题目详情
如图,已知二次函数y1=-x2+
x+c的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为y2=kx+b.
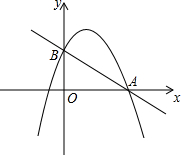
(1)求二次函数y1的解析式及点B的坐标;
(2)由图象写出满足y1<y2的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
| 13 |
| 4 |

(1)求二次函数y1的解析式及点B的坐标;
(2)由图象写出满足y1<y2的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
▼优质解答
答案和解析
(1)将A点坐标代入y1,得
-16+13+c=0.
解得c=3,
二次函数y1的解析式为y=-x2+
x+3,
B点坐标为(0,3);
(2)由图象得直线在抛物线上方的部分,是x<0或x>4,
∴x<0或x>4时,y1<y2;
(3)直线AB的解析式为y=-
x+3,
AB的中点为(2,
)
AB的垂直平分线为y=
x-
当x=0时,y=-
,P1(0,-
),
当y=0时,x=
,P2(
,0),
综上所述:P1(0,-
),P2(
,0),使得△ABP是以AB为底边的等腰三角形.
-16+13+c=0.
解得c=3,
二次函数y1的解析式为y=-x2+
| 13 |
| 4 |
B点坐标为(0,3);
(2)由图象得直线在抛物线上方的部分,是x<0或x>4,
∴x<0或x>4时,y1<y2;
(3)直线AB的解析式为y=-
| 3 |
| 4 |
AB的中点为(2,
| 3 |
| 2 |
AB的垂直平分线为y=
| 4 |
| 3 |
| 7 |
| 6 |
当x=0时,y=-
| 7 |
| 6 |
| 7 |
| 6 |
当y=0时,x=
| 7 |
| 8 |
| 7 |
| 8 |
综上所述:P1(0,-
| 7 |
| 6 |
| 7 |
| 8 |
看了 如图,已知二次函数y1=-x...的网友还看了以下:
若直线y=12x-2与直线y=-14x+a相交于x轴上,则直线y=-14x+a不经过()A.第一象限 2020-03-30 …
(2012•松北区一模)已知反比例函数y=−1x,下列结论不正确的是()A.图象必经过点(一l,2 2020-04-08 …
反比例函数y=kx(k>1)和y=1x在第一象限内的图象如图所示,点P在y=kx的图象上,PC⊥x 2020-04-08 …
如图,点a是反比例函数y等于负x分之2在第二象限内图象上一点,点b是反比例函数y等于x分之4在第一 2020-04-08 …
若一次函数y=(k-1)x+(m+3)的图象经过原点,则下列关系中正确的是Ak=1Bm=-3Ck≠ 2020-04-08 …
一.二次函数的问题1.若函数y=-x+b的图象经过第一,三,四象限,则函数y=ax²+bx-b/8 2020-04-08 …
如图,直线AB是一次函数y=x+a的图象,直线AC是一次函数y=-2x+b的图象,(b》a》0), 2020-05-13 …
1.与抛物线y=-x2+3x-5的形状大小开口方向相同,只有位置不同的抛物线是()A.y=-x2+ 2020-05-13 …
已知点P(x,y)是第一象限内的点,且在直线y=-x+8上,已知点P(x,y)是第一象限...已知 2020-05-14 …
若二次函数y=f(x)的图象过原点,且它的导数y=f′(x)的图象是经过第一、二、三象限的一条直线 2020-05-20 …