如图，在第一象限内，一次函数y=k1x-2的图象与反比例函数y=k2x的图象相交于点A（4，a），与y轴、x轴分别相交于B，C两点，且BC=CA．（1）求反比例函数的解析式；（2）根据图象，试求出在第

Question

如图，在第一象限内，一次函数y=k₁x-2的图象与反比例函数y=(k2)/(x)的图象相交于点A（4，a），与y轴、x轴分别相交于B，C两点，且BC=CA．

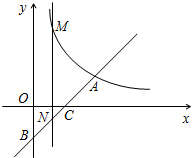
（1）求反比例函数的解析式；
（2）根据图象，试求出在第一象限内，一次函数的值小于反比例函数值的x的取值范围；
（3）若M（m，n）（0<m<4）为反比例函数y=(k2)/(x)图象上一点，过M点作MN⊥x轴交一次函数y=k₁x-2的图象于N点，若以M，N，A为顶点的三角形是直角三角形，求M点的坐标．

Answer 1

（1）过点A作AE⊥x轴于点E，如图所示．

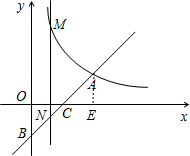
∵AE⊥x轴，BO⊥OC，
∴∠AEC=∠BOC=90°，
在△ACE和△BCO中，

∠AEC=∠BOC

∠ACE=∠BCO

BC=AC

，
∴△ACE≌△BCO（AAS）．
∴AE=BO．
令一次函数y=k₁x-2中x=0，则y=-2，
∴BO=AE=2．
∴点A的坐标为（4，2），
将点A（4，2）代入到反比例函数y=(k2)/(x)中，
2=(k2)/(4)，解得：k₂=8．
∴反比例函数的解析式为y=(8)/(x)．
（2）观察函数图象可知：当0<x<4时，一次函数图象在反比例函数图象下方，
∴在第一象限内，一次函数的值小于反比例函数值的x的取值范围为0<x<4．
（3）∵点M（m，n）（0<m<4）为反比例函数y=(8)/(x)图象上一点，
∴n=(8)/(m)．
∵点A（4，2）在一次函数y=k₁x-2的图象上，
∴2=4k₁-2，解得：k₁=1，
∴一次函数解析式为y=x-2．
∵MN⊥x轴交一次函数y=x-2的图象于N点，
∴点N的坐标为（m，m-2）．
∵以M，N，A为顶点的三角形是直角三角形，
∴AM⊥AN，即(m-2-2)/(m-4)•((8)/(m)-2)/(m-4)=-1，
∴m²-6m+8=（m-2）（m-4）=0，
解得：m₁=2，m₂=4（舍去）．
∴点M的坐标为（2，4）．