早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,点P是AD边上的一个动点,连接PB,过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.(1)求证:△PBQ是等腰直角三角形;
题目详情
如图,在正方形ABCD中,点P是AD边上的一个动点,连接PB,过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.
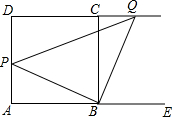
(1)求证:△PBQ是等腰直角三角形;
(2)若PQ2=PB2+PD2+1,求△PAB的面积.

(1)求证:△PBQ是等腰直角三角形;
(2)若PQ2=PB2+PD2+1,求△PAB的面积.
▼优质解答
答案和解析
(1)证明:∵∠QBE=∠PBC,∠QBE+∠QBC=90°,
∴∠PBQ=∠PBC+∠QBC=90°,
∵∠PBC+∠PBA=90°,
∴∠PBA=∠QBC,
在Rt△PAB和Rt△QCB中,
,
∴△PAB≌△QCB(ASA),
∴PB=QB,
∴△PBQ是等腰直角三角形;
(2) 设正方形的边长AB=a,PA=x,
∵△PAB≌△QCB,
∴QC=PA=x,
∴DQ=DC+QC=a+x,PD=AD-PA=a-x,
在Rt△PAB中,PB2=PA2+AB2=x2+a2,
∵PQ2=PB2+PD2+1,
∴(a-x)2+(a+x)2=x2+a2+(a-x)2+1,
解得:2ax=1,
∴ax=
,
∵△PAB的面积S=
PA•PB=
ax=
×
=
.
∴∠PBQ=∠PBC+∠QBC=90°,
∵∠PBC+∠PBA=90°,
∴∠PBA=∠QBC,
在Rt△PAB和Rt△QCB中,
|
∴△PAB≌△QCB(ASA),
∴PB=QB,
∴△PBQ是等腰直角三角形;
(2) 设正方形的边长AB=a,PA=x,
∵△PAB≌△QCB,
∴QC=PA=x,
∴DQ=DC+QC=a+x,PD=AD-PA=a-x,
在Rt△PAB中,PB2=PA2+AB2=x2+a2,
∵PQ2=PB2+PD2+1,
∴(a-x)2+(a+x)2=x2+a2+(a-x)2+1,
解得:2ax=1,
∴ax=
| 1 |
| 2 |
∵△PAB的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
看了 如图,在正方形ABCD中,点...的网友还看了以下:
在等边三角形ABC中,D为线段BC上的动点,连接AD,在角ADC内作角ADE等于60度,交AC边于 2020-05-13 …
把三角尺放在边长1的正方形ABCD上,使直角顶点P在对角线AC上滑动,直角边始终过点B,另一边与射 2020-05-16 …
在△abc中,∠C=90°,∠a,∠b,∠c的对边为a,b,c.求(1)已知a=3.25,∠a=3 2020-07-09 …
在三角形ABC角ABC所对的边分别为abc已知a=2c=3cosB=四分之一求b的值求sinC的值 2020-07-21 …
已知一次函数y=2x+b.(1)如果它的图象与一次函数y=-2x+1和y=x+4的图象的交于同一点 2020-07-25 …
计算:已知a分之1加b分之1=根号5(a不等于b)求b(a-b)分之a减a(a-b)分之计算:已知 2020-08-01 …
1.已知a,b,c满足ab+a+b=bc+b+c=ca+c+a=3求(a+1)(b+1(c+1)的 2020-08-01 …
对电阻求对数后,还有单位吗?大学物理实验:温度传感器的实验中有一个公式是R=R1*EXP(B/T- 2020-08-01 …
1、有一个N边形的内角与外角和的比是9:2,求N边形的边数2、两个多边形边数之比是1:2内角和是3: 2020-10-31 …
阅读:例:已知1/a+1/b=5/a+b,求b/a+a/b的值.因为1/a+1/b=5/a+b,所以 2020-11-15 …