早教吧作业答案频道 -->数学-->
已知抛物线y=-mx2+4x+2m与x轴交于点A(α,0),B(β,0),且1α+1β=-2.(1)求抛物线的解析式;(2)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P
题目详情
已知抛物线y=-mx2+4x+2m与x轴交于点A(α,0),B(β,0),且
+
=-2.
(1)求抛物线的解析式;
(2)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.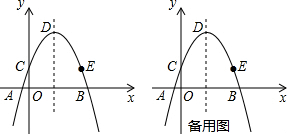
| 1 |
| α |
| 1 |
| β |
(1)求抛物线的解析式;
(2)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.

▼优质解答
答案和解析
(1)由题意可得:α,β是方程-mx2+4x+2m=0的两根,由根与系数的关系可得,
α+β=
,αβ=-2,
∵
+
=-2,
∴
=-2,即
=-2,
解得:m=1,
故抛物线解析式为:y=-x2+4x+2;
(2)∵y=-x2+4x+2=-(x-2)2+6,
∴抛物线的对称轴l为x=2,顶点D的坐标为:(2,6),
又∵抛物线与y轴交点C的坐标为:(0,2),点E与点C关于l对称,
∴E点坐标为:(4,2),
P为抛物线上的点,过点P作PH⊥x轴,垂足为H,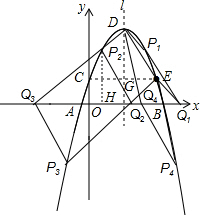
若以点D、E、P、Q为顶点的四边形为平行四边形,则△PHQ≌△DGE,
∴PH=DG=4,
∴|y|=4,
∴当y=4时,-x2+4x+2=4,
解得:x1=2+
,x2=2-
,
当y=-4时,-x2+4x+2=-4,
解得:x3=2+
,x4=2-
,
无法得出以DE为对角线的平行四边形,
故P点的坐标为;(2-
,4),(2+
,4),(2-
,-4),(2+
,-4).
α+β=
| 4 |
| m |
∵
| 1 |
| α |
| 1 |
| β |
∴
| α+β |
| αβ |
| ||
| -2 |
解得:m=1,
故抛物线解析式为:y=-x2+4x+2;
(2)∵y=-x2+4x+2=-(x-2)2+6,
∴抛物线的对称轴l为x=2,顶点D的坐标为:(2,6),
又∵抛物线与y轴交点C的坐标为:(0,2),点E与点C关于l对称,
∴E点坐标为:(4,2),
P为抛物线上的点,过点P作PH⊥x轴,垂足为H,

若以点D、E、P、Q为顶点的四边形为平行四边形,则△PHQ≌△DGE,
∴PH=DG=4,
∴|y|=4,
∴当y=4时,-x2+4x+2=4,
解得:x1=2+
| 2 |
| 2 |
当y=-4时,-x2+4x+2=-4,
解得:x3=2+
| 10 |
| 10 |
无法得出以DE为对角线的平行四边形,
故P点的坐标为;(2-
| 2 |
| 2 |
| 10 |
| 10 |
看了 已知抛物线y=-mx2+4x...的网友还看了以下:
如图所示,水平放置的长为l、距离为d的两平行金属板,极板所加电压为U,一质量为m(重力不计)的带电 2020-04-06 …
如图所示,两块水平放置的平行正对的金属板a、b与电池相连,在距离两板等远的M点有一个带电液滴处于静 2020-04-27 …
物体升高时,其重心在空中的位置一定不变重心嘛,物体受到的重力等效到一个点上.形状规则,质量分布均匀 2020-04-27 …
在平面坐标系中抛物线过A(-4,0)B(0,-4)C(2,0)三点点M第三象限内抛物线上动点,点M 2020-06-14 …
如图所示,两块水平放置的平行正对的金属板a、b与电池相连,在距离两板等远的M点有一个带电液滴处于静 2020-07-15 …
直线l过原点和点(3,5),位于第一象限的点A在直线l上,x轴上有一点B,它的坐标为16,0角AB 2020-07-22 …
n在下m在上m//n,点B,C是直线n上两点,点A是直线m上一点(AB≠AC),在直线m上另找一点 2020-08-01 …
(2013•怀柔区二模)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B 2020-08-03 …
(2010•济宁)如图,是一张宽m的矩形台球桌ABCD,一球从点M(点M在长边CD上)出发沿虚线MN 2020-11-13 …
一质量为M的楔形物体放在倾角为α的固定的光滑斜面上,楔形物体的上表面与水平面平行,再在这个面上放一质 2020-11-25 …