早教吧作业答案频道 -->数学-->
设抛物线y2=4x的焦点为F,准线为l.已知点C在l上,以C为圆心的圆与y轴的正半轴相切于点A.若∠FAC=120°,则圆的方程为.
题目详情
设抛物线y2=4x的焦点为F,准线为l.已知点C在l上,以C为圆心的圆与y轴的正半轴相切于点A.若∠FAC=120°,则圆的方程为___.
▼优质解答
答案和解析
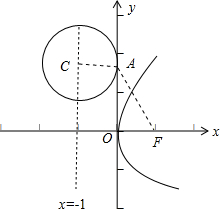 设抛物线y2=4x的焦点为F(1,0),准线l:x=-1,∵点C在l上,以C为圆心的圆与y轴的正半轴相切与点A,
设抛物线y2=4x的焦点为F(1,0),准线l:x=-1,∵点C在l上,以C为圆心的圆与y轴的正半轴相切与点A,
∵∠FAC=120°,∴∠FAO=30°,∴OA=
=
=1,∴OA=
,∴A(0,
),如图所示:
∴C(-1,
),圆的半径为CA=1,故要求的圆的标准方程为 (x+1)2+(y-
)2=1,
故答案为:(x+1)2+(y-
)2=1.
 设抛物线y2=4x的焦点为F(1,0),准线l:x=-1,∵点C在l上,以C为圆心的圆与y轴的正半轴相切与点A,
设抛物线y2=4x的焦点为F(1,0),准线l:x=-1,∵点C在l上,以C为圆心的圆与y轴的正半轴相切与点A,∵∠FAC=120°,∴∠FAO=30°,∴OA=
| OF |
| tan∠FAO |
| 1 | ||||
|
| 3 |
| 3 |
∴C(-1,
| 3 |
| 3 |
故答案为:(x+1)2+(y-
| 3 |
看了 设抛物线y2=4x的焦点为F...的网友还看了以下:
在RT三角形,B=90度,AB=2,tanA=√2/4,以AB两点为焦点的椭圆E过点C,建立适当的 2020-05-13 …
已知中心在原点"焦点在X轴上的椭圆C的离心率e=二分之一"直线l1:x+2y-4=0是椭圆C的切线 2020-05-13 …
已知中心在原点的椭圆C的左焦点F(-3,0),右顶点A(2,0).(1)求椭圆C的标准方程;(2) 2020-05-15 …
中心在原点O,焦点F1、F2在x轴上的椭圆E经过C(2,2),且CF1•CF2=2.(1)求椭圆E 2020-05-15 …
中心在原点O,焦点F1、F2在x轴上的椭圆E经过点C(2,2),且CF1•CF2=2.(Ⅰ)求椭圆 2020-05-15 …
直线l的方程为y=x+3,在l上任取一点P,若过点P且以双曲线12x2-4y2=3的焦点为椭圆的焦 2020-05-15 …
在直线L:x-y+9=0上任取一点p以椭圆x212+y23=1的焦点为焦点作椭圆.(1)p在何处时 2020-05-15 …
椭圆的一个顶点为A(0,-1)焦点在x轴上,若右焦点到直线x-y+2√2=0的距离为3(1)求椭圆 2020-05-16 …
一个圆锥曲线证明题(难度不小哦)在椭圆中,F为焦点,L为其对应准线,AB是长轴的端点,P是椭圆上异 2020-06-13 …
已知A点坐标为(0,8),直线l:x-2y-4=0与y轴交于B点.P为直线l上动点1、求以A点位定 2020-06-14 …