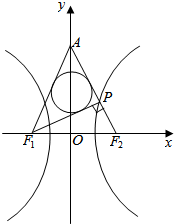
如图，F1，F2为双曲线C：x2a2-y2b2=1（a>0，b>0）的左右焦点，且|F1F2|=2．若双曲线C的右支上存在点P，使得PF1⊥PF2．设直线PF2与y轴交于点A，且△APF1的

Question

如图，F₁，F₂为双曲线C： (x2)/(a2)- (y2)/(b2)=1（a>0，b>0）的左右焦点，且|F₁F₂|=2．若双曲线C的右支上存在点P，使得PF₁⊥PF₂．设直线PF₂与y轴交于点A，且△APF₁的内切圆半径为 (1)/(2)，则双曲线C的离心率为___．

Answer 1

：∵PF₁⊥PF₂，△APF₁的内切圆半径为(1)/(2)，
∴|PF₁|+|PA|-|AF₁|=1，
∴|PF₂|+2a+|PA|-|AF₁|=1，
∴|AF₂|-|AF₁|=1-2a，
∵由图形的对称性知：|AF₂|=|AF₁|，
∴a=(1)/(2)．
∵|F₁F₂|=2，
∴c=1，
∴e=(c)/(a)=2．
故答案为：2．