早教吧作业答案频道 -->数学-->
已知函数f(x)=|x+1|-2|x-a|,a>0.(Ⅰ)当a=1时,求不等式f(x)>1的解集;(Ⅱ)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.
题目详情
已知函数f(x)=|x+1|-2|x-a|,a>0.
(Ⅰ)当a=1时,求不等式f(x)>1的解集;
(Ⅱ)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.
(Ⅰ)当a=1时,求不等式f(x)>1的解集;
(Ⅱ)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.
▼优质解答
答案和解析
 (Ⅰ)当a=1时,不等式f(x)>1,即|x+1|-2|x-1|>1,
(Ⅰ)当a=1时,不等式f(x)>1,即|x+1|-2|x-1|>1,
即
①,或
②,
或
③.
解①求得x∈∅,解②求得
<x<1,解③求得1≤x<2.
综上可得,原不等式的解集为(
,2).
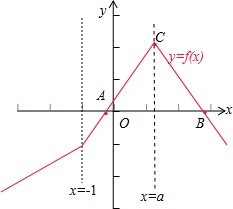
(Ⅱ)函数f(x)=|x+1|-2|x-a|=
,
由此求得f(x)的图象与x轴的交点A (
,0),
B(2a+1,0),
故f(x)的图象与x轴围成的三角形的第三个顶点C(a,a+1),
由△ABC的面积大于6,
可得
[2a+1-
]•(a+1)>6,求得a>2.
故要求的a的范围为(2,+∞).
 (Ⅰ)当a=1时,不等式f(x)>1,即|x+1|-2|x-1|>1,
(Ⅰ)当a=1时,不等式f(x)>1,即|x+1|-2|x-1|>1,即
|
|
或
|
解①求得x∈∅,解②求得
| 2 |
| 3 |
综上可得,原不等式的解集为(
| 2 |
| 3 |
(Ⅱ)函数f(x)=|x+1|-2|x-a|=
|
由此求得f(x)的图象与x轴的交点A (
| 2a-1 |
| 3 |
B(2a+1,0),
故f(x)的图象与x轴围成的三角形的第三个顶点C(a,a+1),
由△ABC的面积大于6,
可得
| 1 |
| 2 |
| 2a-1 |
| 3 |
故要求的a的范围为(2,+∞).
看了 已知函数f(x)=|x+1|...的网友还看了以下:
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
已知集合A={x︱0<ax+1≤5},集合B={x︱-1/2<x≤2}.(1)若A包含于B,求实数 2020-04-05 …
设三阶实对称矩阵A的特征值分别为0,1,1,α1=1a0,α2=1−1a是A的两个不同的特征向量, 2020-04-13 …
3 2—— - ——=a-1 2-aa^2—— - a -b=a-b2 x-1(1 - ——)÷— 2020-05-13 …
S(2n-1)=n(a1+a(2n-1))/2的推出方法是什么?是不是S(2n-1)=(2n-1) 2020-05-14 …
1.DIMENSIONA(2,3)A=175A怎么能175?不是最大是6吗?A(2,2)=2*A( 2020-06-12 …
求坐标的题目,我每次不知道为啥算出的答案都不同(1)A(0,-1,2),B(2,y,5)|AB|= 2020-06-14 …
下列各式计算正确的是?(我没找到)A.(a+1)^2=a^2+1B.a^2+a^3=a^5C.a^ 2020-07-09 …
1.在下列对应中,哪些是映射,哪些映射是函数,哪些不是?为什么?(1)设A={1,2,3,4},B 2020-07-30 …
怎么化能得到cos(A+C)*cos(A-C)=-1/2*cos(A-C)?好像是用积化和差的公式 2020-08-02 …