早教吧作业答案频道 -->数学-->
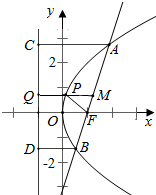
设抛物线y2=4x的焦点为F,A,B两点在抛物线上,且A,B,F三点共线,过AB的中点M作y轴的垂线与抛物线在第一象限内交于点P,若|PF|=32,则M点的横坐标为.
题目详情
设抛物线y2=4x的焦点为F,A,B两点在抛物线上,且A,B,F三点共线,过AB的中点M作y轴的垂线与抛物线在第一象限内交于点P,若|PF|=
,则M点的横坐标为___.
| 3 |
| 2 |
▼优质解答
答案和解析
 ∵抛物线方程为y2=4x,
∵抛物线方程为y2=4x,
∴抛物线的焦点为F(1,0),准线为l:x=-1,
设A(x1,y1),B(x2,y2),直线AB的方程为y=k(x-1),
代入抛物线方程消去y,得k2x2-(2k2+4)x+k2=0,
∴x1+x2=
,x1x2=1,
∵过AB的中点M作准线的垂线与抛物线交于点P,
∴设P的坐标为(x0,y0),可得y0=
(y1+y2),
∵y1=k(x1-1),y2=k(x2-1),
∴y1+y2=k(x1+x2)-2k=k•
-2k=
,
得到y0=
,所以x0=
,可得M(
,
).
∵|PF|=
,
∴
=
,解之得k2=2,
因此x1+x2=
=4,
∴M点的横坐标为
(x1+x2)=2,
故答案为:2
 ∵抛物线方程为y2=4x,
∵抛物线方程为y2=4x,∴抛物线的焦点为F(1,0),准线为l:x=-1,
设A(x1,y1),B(x2,y2),直线AB的方程为y=k(x-1),
代入抛物线方程消去y,得k2x2-(2k2+4)x+k2=0,
∴x1+x2=
| 2k2+4 |
| k2 |
∵过AB的中点M作准线的垂线与抛物线交于点P,
∴设P的坐标为(x0,y0),可得y0=
| 1 |
| 2 |
∵y1=k(x1-1),y2=k(x2-1),
∴y1+y2=k(x1+x2)-2k=k•
| 2k2+4 |
| k2 |
| 4 |
| k |
得到y0=
| 2 |
| k |
| 1 |
| k2 |
| 2 |
| k |
| 1 |
| k2 |
∵|PF|=
| 3 |
| 2 |
∴
(1-
|
| 3 |
| 2 |
因此x1+x2=
| 2k2+4 |
| k2 |
∴M点的横坐标为
| 1 |
| 2 |
故答案为:2
看了 设抛物线y2=4x的焦点为F...的网友还看了以下:
一个一公斤质量物体垂直下落10米的时间是一定的,如果在物体每下落一米就停止再继续下落,这样物体分1 2020-05-14 …
因标的物质量不符合质量要求,致使不能实现合同目的的,买受人可以拒绝接受标的物或者解 2020-05-22 …
()是指保险标的的发生保险事故保险人赔付被保险人全部财产损失后,可直接取得保险标的物的物权的 2020-05-22 …
在我国,买卖合同标的物所有权的转移时间是()。A.特定物在买卖合同订立时转移B.种类物在标的物交付 2020-06-04 …
及于主物,《中华人民共和国合同法》第一百六十四条:因标的物的主物不符合约定而解除合同的,解除合同的 2020-06-17 …
一个关于抛物线和椭圆的问题抛物线顶点在原点,它的准线过椭圆X^2/a^2+Y^2/b^2=1(a> 2020-06-21 …
设O为坐标原点,曲线X^2+Y^2+2X-6Y+1=0 上有2点P Q,满足关于直线X+MY+4= 2020-06-27 …
一个物体高1米,当倾斜45度后有多高一个物体垂直高1米,当物体倾斜到45度后该物体有多高?该物体倾斜 2020-11-05 …
乙二胺四乙酸二钠纯度标准物质如何配制成0.01摩尔每升标准溶液如何将乙二胺四乙酸二钠纯度标准物质(粉 2020-11-29 …
下列行为中属于动物对植物生活产生消极作用的是()A.许多昆虫能为绿色开花植物传粉B.动物的皮毛能粘附 2020-12-25 …