早教吧作业答案频道 -->数学-->
在平面直角坐标系中,抛物线y=12x2经过点A(x1,y1)、C(x2,y2),其中x1、x2是方程x2-2x-8的两根,且x1<x2,过点A的直线l与抛物线只有一个公共点(1)求A、C两点的坐标;(2)求直线l的解
题目详情
在平面直角坐标系中,抛物线y=
x2经过点A(x1,y1)、C(x2,y2),其中x1、x2是方程x2-2x-8的两根,且x1<x2,过点A的直线l与抛物线只有一个公共点
(1)求A、C两点的坐标;
(2)求直线l的解析式;
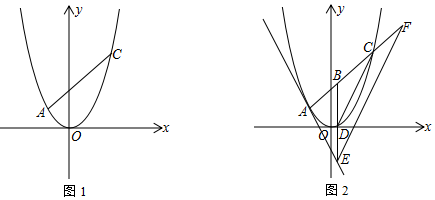
(3)如图2,点B是线段AC上的动点,若过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,过点E作DC的平行线EF与直线AC相交于点F,求BF的长.
| 1 |
| 2 |
(1)求A、C两点的坐标;
(2)求直线l的解析式;
(3)如图2,点B是线段AC上的动点,若过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,过点E作DC的平行线EF与直线AC相交于点F,求BF的长.

▼优质解答
答案和解析
(1)∵x1、x2是方程x2-2x-8的两根,且x12,
∴x1=-2,x2=4,
∴A(-2,2),C(4,8);
(2)设直线l的解析式为y=kx+b,
∵A(-2,2)在直线l上,
∴2=-2k+b,
∴b=2k+2,
∴直线l的解析式为y=kx+2k+2①,
∵抛物线y=
x2②,
联立①②化简得,x2-2kx-4k-4=0,
∵直线l与抛物线只有一个公共点,
∴△=(2k)2-4(-4k-4)=4k2+16k+16=4(k2+4k+4)=4(k+2)2=0,
∴k=-2,
∴b=2k+2=-2,
∴直线l的解析式为y=-2x-2;
(3)由(1)知,A(-2,2),C(4,8),
∴直线AC的解析式为y=x+4,
设点B(m,m+4),
∵(4.8),
∴BC=
|m-4|=
(4-m)
∵过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,
∴D(m,
m2),E(m,-2m-2),
∴BD=m+4-
m2,BE=m+4-(-2m-2)=3m+6,
∵DC∥EF,
∴△BDC∽△BEF,
∴
=
,
∴
=
,
∴BF=6
.
∴x1=-2,x2=4,
∴A(-2,2),C(4,8);
(2)设直线l的解析式为y=kx+b,
∵A(-2,2)在直线l上,
∴2=-2k+b,
∴b=2k+2,
∴直线l的解析式为y=kx+2k+2①,
∵抛物线y=
| 1 |
| 2 |
联立①②化简得,x2-2kx-4k-4=0,
∵直线l与抛物线只有一个公共点,
∴△=(2k)2-4(-4k-4)=4k2+16k+16=4(k2+4k+4)=4(k+2)2=0,
∴k=-2,
∴b=2k+2=-2,
∴直线l的解析式为y=-2x-2;
(3)由(1)知,A(-2,2),C(4,8),
∴直线AC的解析式为y=x+4,
设点B(m,m+4),
∵(4.8),
∴BC=
| 2 |
| 2 |
∵过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,
∴D(m,
| 1 |
| 2 |
∴BD=m+4-
| 1 |
| 2 |
∵DC∥EF,
∴△BDC∽△BEF,
∴
| BD |
| BE |
| BC |
| BF |
∴
m+4-
| ||
| 3m+6 |
| ||
| BF |
∴BF=6
| 2 |
看了 在平面直角坐标系中,抛物线y...的网友还看了以下:
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成 2020-04-27 …
已知;抛物线Y=ax^2+2x+c,对称轴位直线x=-1,抛物线与y轴交与点c抛物线与Y轴交于点C 2020-05-16 …
已知双曲线:y=k/x与抛物线:y=ax的平方+bx+c(a≠0)的图像与x轴交于M(2,0),N 2020-05-16 …
若抛物线y=ax²+bx+c与x轴交于AB两点,与y轴交于点C,我们称△ABC为抛物线的奠基三角形 2020-05-16 …
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点为B(2,1),且过点A(0, 2020-06-14 …
将抛物线y=2(x-4)2-1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解 2020-06-27 …
抛物线y=x^2上求一点,使该点的切线与直线y=o,x=8相围成三角形面积最大 2020-07-02 …
正方形的边长为5,若边成增加X,那么面织增加Y,那么Y与X的关系是我做觉得对,还有若抛物线Y=aX 2020-07-11 …
如图,P是抛物线C:y=2x2-8x+8对称轴上的一个动点,直线x=k平行于y轴,分别与直线y=x、 2020-11-04 …
抛物线和圆的交点不对称如题,已知圆方程x^2+y^2=8,抛物线y^2=2x,将两方程联立后解出了两 2020-11-21 …