设倾斜角为α的直线l经过抛物线C：y2=2px（p>0）的焦点F，与抛物线C交于A，B两点，设点A在x轴上方，点B在x轴下方．若|AF||BF|=m，则cosα的值为（）A.m-1m+1B.mm+1C.m-1mD.2mm+1

Question

设倾斜角为α的直线l经过抛物线C：y²=2px（p>0）的焦点F，与抛物线C交于A，B两点，设点A在x轴上方，点B在x轴下方．若

(|AF|)/(|BF|)=m，则cosα的值为（　　）

A.

(m-1)/(m+1)

B.

(m)/(m+1)

C.

(m-1)/(m)

D.

(2√(m))/(m+1)

Answer 1

设抛物线y²=2px（p>0）的准线为l：x=-(p)/(2)．
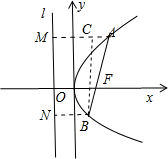
如图所示，分别过点A，B作AM⊥l，BN⊥l，垂足为M，N．
在三角形ABC中，∠BAC等于直线AB的倾斜角α，
由(|AF|)/(|BF|)=m，|AF|=m|BF|，丨AB丨=丨AF丨+丨BF丨=（m+1）丨BF丨，
根据抛物线的定义得：|AM|=丨AF丨=m|BF|，丨BN丨=丨BF丨，
∴|AC|=丨AM丨-丨MC丨=m|BF|-丨BF丨=（m-1）丨BF丨，
在直角三角形ABC中，cosα=cosα∠BAC=(丨AC丨)/(丨AB丨)=((m-1)丨BF丨)/((m+1)丨BF丨)=(m-1)/(m+1)；
故选A．