早教吧作业答案频道 -->数学-->
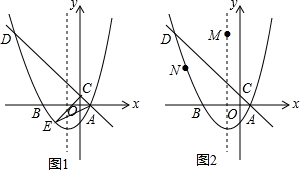
如图1,在平面直角坐标系中,直线y=-x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(-4,5),并与y轴交于点C,抛物线的对称轴为直线x=-1,且抛物线与x轴交于另一点B.(1)求该抛物
题目详情
如图1,在平面直角坐标系中,直线y=-x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(-4,5),并与y轴交于点C,抛物线的对称轴为直线x=-1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=-1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=-1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.

▼优质解答
答案和解析
(1)∵A(1,0),抛物线的对称轴为x=-1,
∴B(-3,0).
设抛物线的解析式为y=a(x+3)(x-1),
将点D的坐标代入得:5a=5,解得a=1,
∴抛物线的解析式为y=x2+2x-3.
(2)如图1所示:过点E作EF∥y轴,交AD与点F,过点C作CH⊥EF,垂足为H.
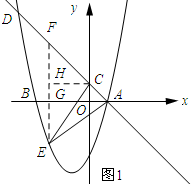
设点E(m,m2+2m-3),则F(m,-m+1).
∴EF=-m+1-m2-2m+3=-m2-3m+4
∴△ACE的面积=△EFA的面积-△EFC的面积=
EF•AG-
EF•HC=
EF•OA=-
(m+
)2+
.
∴△ACE的面积的最大值为
.
(3)当AD为平行四边形的对角线时.
设点M的坐标为(-1,a),点N的坐标为(x,y).
∵平行四边的对角线互相平分,
∴
=
,
=
.
解得:x=-2,5-a.
将点N的坐标代入抛物线的解析式得:5-a=-3,
∴a=8.
∴点M的坐标为(-1,8).
当AD为平行四边形的边时.
设点M的坐标为(-1,a).
∵四边形MNAD为平行四边形,
∴点N的坐标为(-6,a+5)或(4,a-5).
∵将x=-6,y=a+5代入抛物线的解析式得:a+5=36-12-3,解得:a=16,
∴M(-1,16).
将x=4,y=a-5代入抛物线的解析式得:a-5=16+8-3,解得:a=26,
∴M(-1,26).
综上所述,当点M的坐标为(-1,26)或(-1,16)或(-1,8)时,以点A,D,M,N为顶点的四边形能成为平行四边形.
∴B(-3,0).
设抛物线的解析式为y=a(x+3)(x-1),
将点D的坐标代入得:5a=5,解得a=1,
∴抛物线的解析式为y=x2+2x-3.
(2)如图1所示:过点E作EF∥y轴,交AD与点F,过点C作CH⊥EF,垂足为H.

设点E(m,m2+2m-3),则F(m,-m+1).
∴EF=-m+1-m2-2m+3=-m2-3m+4
∴△ACE的面积=△EFA的面积-△EFC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
∴△ACE的面积的最大值为
| 25 |
| 8 |
(3)当AD为平行四边形的对角线时.
设点M的坐标为(-1,a),点N的坐标为(x,y).
∵平行四边的对角线互相平分,
∴
| -1+x |
| 2 |
| 1+(-4) |
| 2 |
| y+a |
| 2 |
| 0+5 |
| 2 |
解得:x=-2,5-a.
将点N的坐标代入抛物线的解析式得:5-a=-3,
∴a=8.
∴点M的坐标为(-1,8).
当AD为平行四边形的边时.
设点M的坐标为(-1,a).
∵四边形MNAD为平行四边形,
∴点N的坐标为(-6,a+5)或(4,a-5).
∵将x=-6,y=a+5代入抛物线的解析式得:a+5=36-12-3,解得:a=16,
∴M(-1,16).
将x=4,y=a-5代入抛物线的解析式得:a-5=16+8-3,解得:a=26,
∴M(-1,26).
综上所述,当点M的坐标为(-1,26)或(-1,16)或(-1,8)时,以点A,D,M,N为顶点的四边形能成为平行四边形.
看了 如图1,在平面直角坐标系中,...的网友还看了以下:
帮我解决一些口算吧,35+26.53-35.12*8.84/3.2.1+0.7.3.1+0.4.6 2020-04-07 …
14.有一份某品牌饮用水理化指标:含有成分(含量):钙(大于4.0%),镁(大于0.5%),钾(大 2020-05-14 …
0.8x+3.2=7.212.5-3x=6.556.4÷x+14.8=24.21.2(x-0.64 2020-05-16 …
随机取点P(x,y),其中0小于等于x小于等于4,0小于等于y小于等于4.)(1)求当x,y属于Z 2020-06-27 …
1.已知方程x^2-(m+1)x+4=0的两根都落在0,3,求m的取值范围2.求m的取值范围,使关 2020-06-27 …
10-2.65=0.9×0.08=528-349=6+14.4=24÷0.04=12.34-2.3 2020-07-18 …
已知集合A={p|x^2+2(p-1)x+1=0,x∈R},求集合B={y|y=2x-1,x∈A} 2020-08-01 …
直接写得数.0.2×0.14﹦3.4+1.6﹦0.73-0.3﹦7.1+1.09=3.5×20﹦30 2020-11-19 …
直接写出得数7.98+0.3=5-2.6=1.4×0.5=3.2÷0.16=1÷0.25=0.7×0 2020-11-19 …
1已知关于x的方程x^2+bx+a=0有一个根是-a(a不等于0)则a-b的值为2方程(k-1)x^ 2020-12-31 …